题目内容
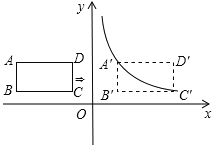
【题目】如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A（
，
），AB=1，AD=2．
（1）直接写出B、C、D三点的坐标；
（2）将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数
（
）的图象上，得矩形A′B′C′D′．求矩形ABCD的平移距离m和反比例函数的解析式．
【答案】（1）B（
，
），C（
，），D（，
）；（2）m=4，
．
【解析】
试题分析：（1）由矩形的性质即可得出结论；
（2）根据平移的性质将矩形ABCD向右平移m个单位，得到A′（
，
），C（
，），由点A′，C′在反比例函数
（
）的图象上，得到方程
，即可求得结果．
试题解析：（1）∵四边形ABCD是矩形，∴AB=CD=1，BC=AD=2，∵A（，），AD∥x轴，∴B（，），C（，），D（，）；
（2）∵将矩形ABCD向右平移m个单位，∴A′（，），C（，），∵点A′，C′在反比例函数（）的图象上，∴，解得：m=4，∴A′（1，），∴
，∴矩形ABCD的平移距离m=4，反比例函数的解析式为：．
练习册系列答案
名校课堂系列答案
相关题目
