题目内容
 如图,在直角三角形ACB中,∠ACB=90°,AC=3cm,BC=4cm,CD为斜边AB上的高,则CD的长度为________cm.
如图,在直角三角形ACB中,∠ACB=90°,AC=3cm,BC=4cm,CD为斜边AB上的高,则CD的长度为________cm.
2.4
分析:在直角三角形ACB中,由AC及BC的长,利用勾股定理求出斜边AB的长,由CD为斜边AB边上的高,直角三角形ABC的面积可以由斜边AB与CD乘积的一半来求,也可以由两直角边乘积的一半来求,根据面积相等可列出关系式,将AC,BC及AB的长代入即可求出CD的长.
解答:∵在直角三角形ACB中,∠ACB=90°,AC=3cm,BC=4cm,
∴根据勾股定理得:AB= =5cm,
=5cm,
又∵CD为斜边AB上的高,
∴S△ABC= AC•BC=
AC•BC= CD•AB,
CD•AB,
则CD= =2.4cm.
=2.4cm.
故答案为:2.4
点评:此题考查了勾股定理的运用,以及三角形面积的求法,其中利用勾股定理求出斜边AB的长是本题的突破点.
分析:在直角三角形ACB中,由AC及BC的长,利用勾股定理求出斜边AB的长,由CD为斜边AB边上的高,直角三角形ABC的面积可以由斜边AB与CD乘积的一半来求,也可以由两直角边乘积的一半来求,根据面积相等可列出关系式,将AC,BC及AB的长代入即可求出CD的长.
解答:∵在直角三角形ACB中,∠ACB=90°,AC=3cm,BC=4cm,
∴根据勾股定理得:AB=
 =5cm,
=5cm,又∵CD为斜边AB上的高,
∴S△ABC=
 AC•BC=
AC•BC= CD•AB,
CD•AB,则CD=
 =2.4cm.
=2.4cm.故答案为:2.4
点评:此题考查了勾股定理的运用,以及三角形面积的求法,其中利用勾股定理求出斜边AB的长是本题的突破点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
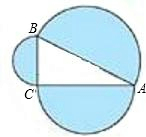 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
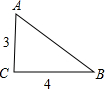
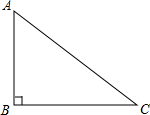 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.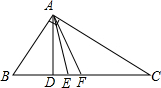 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线, 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=