题目内容
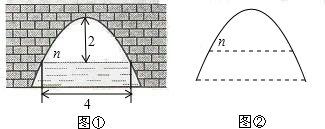
如图，抛物线形的拱桥在正常水位时，水面AB的宽为20m.涨水时水面上升了3m，达到了警戒水位，这时水面宽CD＝10m.
（1）求抛物线的解析式；
（2）当水位继续以每小时0.2m的速度上升时，再经过几小时就到达拱顶？
（1）若以AB所在直线为x轴，AB中点为原点，此时抛物线解析式为
（2）经过5小时到达拱顶
解析试题分析：（1）以AB所在直线为x轴，AB中点为原点，依题意得A（-10,0）B（10,0）C（-5,3），设函数解析式为
，将各点代入可得
，
，即
（2）由于，即顶点纵坐标为4，即拱桥顶点距离AB为4m，所以距离CD为1m，每小时0.2m上升，所以经过5小时候，达到拱顶
考点：三点法求抛物线的解析式
点评：本题难度不大，答案不唯一，不同的坐标系，有不同的解析式，但是第二问的答案是统一的。做此类题目时，一般以中线所在直线为y轴
练习册系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
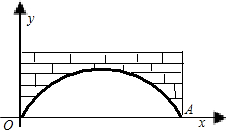如图，有一座抛物线形的拱桥，桥下的正常水位为OA，此时水面宽为40米，水面离桥的最大高度为16米，则拱桥所在的抛物线的解析式为
