Question

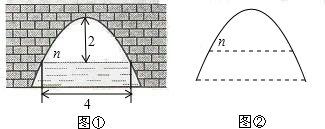
如图①是抛物线形拱桥，当水面在n时，拱顶离水面2米，水面宽4米．
（1）求出拱桥的抛物线解析式；
（2）若水面下降2.5米，则水面宽度将增加多少米？（图②是备用图）

Answer 1

分析：①由题目分析可以知道，应先建立一个直角坐标系，根据三点法写出这个二次函数的解析式，在进行解答．
②求出水面下降2.5米时y的值，再代入原函数解出x的值，与原来水面宽度进行比较求得宽度增加的值．

解答：解：（1）建立如图的直角坐标系，
设拱桥的抛物线解析式为：
y=ax²（a≠0），
将点（2，-2）代入得：4a=-2，
解得：a=-

1

2

，
∴拱桥的抛物线解析式为y=-

1

2

x2，
答：拱桥的抛物线解析式为y=-

1

2

x2．

（2）由题意得：
当y=-4.5时，-

1

2

x2=-4.5，
解得：x=±3，
∴此时水面宽度为6米，
∴水面宽度将增加2米．
答：水面宽度将增加2米．
故答案为①拱桥的抛物线解析式为y=-

1

2

x2，
②水面宽度将增加2米．

点评：本题的解题关键在于坐标系的建立，以及抛物线解析式的列出．