题目内容
从只装有4个红球的袋中随机摸出一球，若摸到白球的概率是P1，摸到红球的概率是P2，则 （ ）
A．P1=1，P2=1
B．P1=0，P2=1
C．P1=0，P2=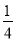
D．P1=P2=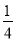
练习册系列答案
世纪百通期末金卷系列答案
相关题目
世纪百通期末金卷系列答案题目内容
从只装有4个红球的袋中随机摸出一球，若摸到白球的概率是P1，摸到红球的概率是P2，则 （ ）
A．P1=1，P2=1
B．P1=0，P2=1
C．P1=0，P2=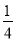
D．P1=P2=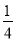
世纪百通期末金卷系列答案
， 
， 
，…都是边长为2的等边三角形，边
在
轴上，点
， 
， 
，…都在直线
上，则
的坐标是（ ）
） B. (2017
,2017)
,2019)
