题目内容
1.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点,①在图1中画出边长分别为:3,2$\sqrt{2}$,$\sqrt{5}$的三角形(不写画法);②在图2中画出边长分别为$\sqrt{13}$,4,$\sqrt{13}$,4的平行四边形(不写画法).
分析 ①本题中2$\sqrt{2}$实际上是直角边长为2和2的三角形的斜边长,$\sqrt{5}$实际上是直角边长为2和1的矩形的三角形的斜边长,据此可找出所求的三角形;
②本题中$\sqrt{13}$实际上是直角边长为3和2的三角形的斜边长,然后据此画出平行四边形.
解答 解:①如图1所示:
②如图2所示:
点评 考查了勾股定理,关键是确定三角形的边长和平行四边形的邻边长,然后根据边长画出所求的三角形和平行四边形.

练习册系列答案
相关题目
13.下列各式由左边到右边的变形,是因式分解的是( )
①(a+3)(a-3)=a2-9 ②m2-4=(m+2)(m-2)
③a2-b2+1=(a+b)(a-b)+1 ④2mR+2mr=2m(R+r)
①(a+3)(a-3)=a2-9 ②m2-4=(m+2)(m-2)
③a2-b2+1=(a+b)(a-b)+1 ④2mR+2mr=2m(R+r)
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
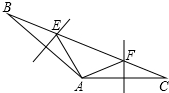 如图,在△ABC中,AB和AC的垂直平分线分别交BC于E、F,若∠BAC=130°,则∠EAF=80°.
如图,在△ABC中,AB和AC的垂直平分线分别交BC于E、F,若∠BAC=130°,则∠EAF=80°.