Question

【题目】已知抛物线，顶点为A，且经过点，点．

（1）求抛物线的解析式；

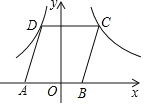
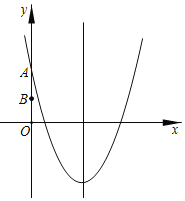
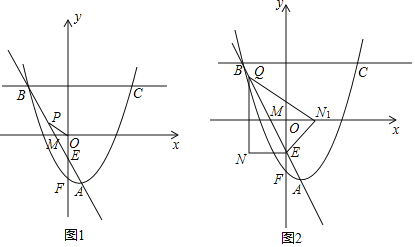
（2）如图1，直线AB与x轴相交于点M，y轴相交于点E，抛物线与y轴相交于点F，在直线AB上有一点P，若∠OPM＝∠MAF，求△POE的面积；

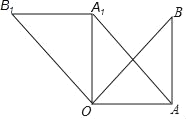
（3）如图2，点Q是折线A﹣B﹣C上一点，过点Q作QN∥y轴，过点E作EN∥x轴，直线QN与直线EN相交于点N，连接QE，将△QEN沿QE翻折得到△QEN1，若点N1落在x轴上，请直接写出Q点的坐标．

Answer 1

【答案】（1）；（2）或；（3）（﹣，）或（﹣，2）或（，2）．

【解析】

（1）将点B坐标代入解析式求得a的值即可；

（2）由∠OPM＝∠MAF知OP∥AF，据此证△OPE∽△FAE得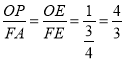，即OP＝FA，设点P（t，﹣2t﹣1），列出关于t的方程解之可得；

（3）分点Q在AB上运动、点Q在BC上运动且Q在y轴左侧、点Q在BC上运动且点Q在y轴右侧这三种情况分类讨论即可得．

（1）把点代入，

解得：a＝1，

∴抛物线的解析式为：；

（2）由知顶点A（，﹣2），

设直线AB解析式为：y＝kx+b，代入点A，B的坐标，

得： ，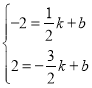

解得：，

∴直线AB的解析式为：y＝﹣2x﹣1，

易求E（0，﹣1），，，

∵∠OPM＝∠MAF，

∴OP∥AF，

∴△OPE∽△FAE，

∴，

∴,

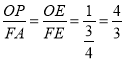设点P（t，﹣2t﹣1），则：

解得，，

∵△POE的面积＝OE|t|，

∴△POE的面积为或．

（3）若点Q在AB上运动，如图1，

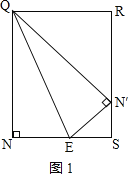
设Q（a，﹣2a﹣1），则NE＝﹣a、QN＝﹣2a，

由翻折知QN′＝QN＝﹣2a、N′E＝NE＝﹣a，

由∠QN′E＝∠N＝90°易知△QRN′∽△N′SE，

∴，即，

∴QR＝2，ES＝，

由NE+ES＝NS＝QR可得﹣a+＝2，

解得：a＝﹣，

∴Q（﹣，）；

若点Q在BC上运动，且Q在y轴左侧，如图2，

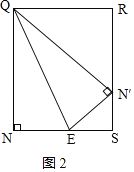
设NE＝a，则N′E＝a，

易知RN′＝2、SN′＝1、QN′＝QN＝3，

∴QR＝、SE＝﹣a，

在Rt△SEN′中，（﹣a）2+12＝a2，

解得：a＝，

∴Q（﹣，2）；

若点Q在BC上运动，且点Q在y轴右侧，如图3，

设NE＝a，则N′E＝a，

易知RN′＝2，SN′＝1，QN′＝QN＝3，

∴QR＝，SE＝﹣a，

在Rt△SEN′中，（﹣a）2+12＝a2，

解得：a＝，

∴Q（，2）．

综上，点Q的坐标为（﹣，））或（﹣，2）或（，2）．