题目内容
如图，AB∥CD，∠B=68
，∠E=20，则∠D的度数为 . 
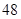
解析试题分析：先根据平行线的性质求得∠CFE的度数，再根据三角形外角的性质求解即可.
∵AB∥CD，∠B=68
∴∠CFE=∠B=68
∵∠E=20
∴∠D=∠CFE-∠E=48.
考点：平行线的性质，三角形外角的性质
点评：解题的关键是熟练掌握三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和.
练习册系列答案
相关题目
题目内容
如图，AB∥CD，∠B=68，∠E=20，则∠D的度数为 .
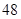
解析试题分析：先根据平行线的性质求得∠CFE的度数，再根据三角形外角的性质求解即可.
∵AB∥CD，∠B=68
∴∠CFE=∠B=68
∵∠E=20
∴∠D=∠CFE-∠E=48.
考点：平行线的性质，三角形外角的性质
点评：解题的关键是熟练掌握三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和.
23、如图，AB∥CD，∠A=90°，AB=2，BC=3，CD=1，E是AD中点．求证：CE⊥BE．
如图，AB∥CD，AD与BC相交于点E，如果AB=2，CD=6，AE=1，那么DE=
4、如图，AB∥CD，∠C=80°，∠CAD=60°，则∠BAD的度数等于（ ）
34、如图，AB∥CD，P是BC上的一个动点，设∠CDP=∠1，∠CPD=∠2，请你猜想出∠1、∠2与∠B之间的关系，并说明理由．
如图，AB∥CD，∠1=58°，则∠2的度数是（ ）