题目内容
在宿州十一中校园文化艺术节中,九年级十班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
(1);(2) 【解析】试题分析:(1)直接根据概率公式求解; (2)画树状图展示所有12种等可能的结果数,再找出刚好是一男生一女生的结果数,然后根据概率公式求解. 试题解析:(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,刚好是男生的概率==; (2)画树状图为: 共有12种等可能的结果数,其中刚好是一男生一女生的结果数为6, 所以刚好是一男生一女生的...如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)求证:四边形BECF是菱形;
(2)若四边形BECF为正方形,求∠A的度数.
万达旅行社为吸引市民组团去黄山风景区旅游,推出了如下的收费标准:

宿州高铁新区组织员工去黄山风景区旅游,共支付给万达旅行社旅游费用27 000元,请问该单位这次共有多少员工去黄山风景区旅游?
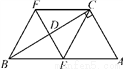
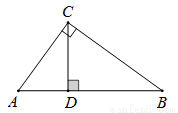
查看答案如图,Rt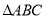 中,
中, 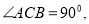 CD是斜边AB的高.
CD是斜边AB的高.
求证: 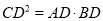 .
.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-2,1).
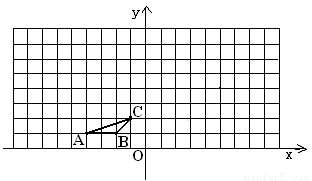
(1)画出△ABC绕C点顺时针旋转90°后得到的△A1B1C1并写出A1点的坐标;
(2)以原点O为位似中心,位似比为2,在第二象限内作△ABC的位似图形△A2B2C2,并写出C2的坐标.
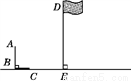
查看答案如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案下列根式中,不能与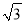 合并的是 ( )
合并的是 ( )
A. 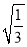 B.
B. 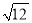 C.
C. 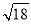 D.
D. 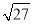
若x2﹣kxy+9y2是一个完全平方式,则k的值为( )
A. 3 B. ±6 C. 6 D. +3
查看答案下列运算正确的是( )
A. 3x2+2x3=5x5 B. (π﹣3.14)0=0 C. 3﹣2=﹣6 D. (x3)2=x6
查看答案如图所示,有一个长方体,它的长、宽、高分别为5cm,3cm,4cm.在顶点A处有一只蚂蚁,它想吃到与顶点A相对的顶点B的食物.
(1)请画出该蚂蚁沿长方体表面爬行的三条线路图(即平面展开图);
(2)已知蚂蚁沿长方体表面爬行的速度是1cm/s,问蚂蚁能否在8秒内获取到食物?
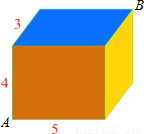
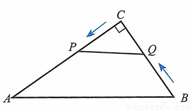
为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
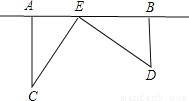
如图,根据要求回答下列问题:
(1)点A关于y轴对称点A′的坐标是 ;点B关于y轴对称点B′的坐标是
(2)作出△ABC关于y轴对称的图形△A′B′C′(不要求写作法)
(3)求△ABC的面积.
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
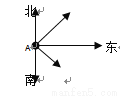
A、25海里 B、30海里 C、35海里 D、40海里
D 【解析】 试题分析:根据方位角可知两船所走的方向正好构成了直角.然后根据路程=速度×时间,得两条船分别走了32,24.再根据勾股定理,即可求得两条船之间的距离. ∵两船行驶的方向是东北方向和东南方向, ∴∠BAC=90°, 两小时后,两艘船分别行驶了16×2=32,12×2=24海里, 根据勾股定理得:(海里), 故选D.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, 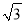 ),则点C的坐标为( )
),则点C的坐标为( )
A. (﹣ ,1) B. (﹣1,
,1) B. (﹣1, 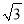 ) C. (
) C. (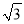 ,1) D. (﹣
,1) D. (﹣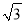 ,﹣1)
,﹣1)
在Rt△ABC中,∠C=90°,∠A, ∠B, ∠C所对的边分别为a,b,c, 已知a∶b=3∶4,c=10,则△ABC的面积为( )
A. 24 B. 12 C. 28 D. 30
查看答案.如图,等边△ABC边长为3cm,将△ABC沿AC向右平移1cm,得到△DEF,则四边形ABEF的周长( )
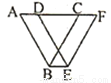
A. 9cm B. 10cm C. 11cm D. 12cm
查看答案点M(﹣3,﹣5)是由N先向上平移4个单位,再向左平移3个单位而得到,则点N的坐标为( )
A.(0,﹣9) B.(﹣6,﹣1) C.(1,﹣2) D.(1,﹣8)
查看答案无理数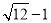 的大小在以下两个整数之间( )
的大小在以下两个整数之间( )
A. 1与2 B. 2与3 C. 3与4 D. 4与5
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列式子正确的是( )
A. 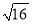 =±4 B. ±
=±4 B. ±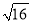 =4 C.
=4 C. 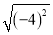 =-4 D. ±
=-4 D. ±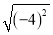 =±4
=±4
下列二次根式中的最简二次根式是 ( )
A. 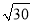 B.
B. 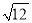 C.
C. 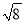 D.
D. 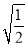
在实数0.333…,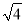 ,
, 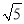 ,-π,3.1415,2.010010001…(相邻两个1之间0的个数逐渐增加)中,无理数有( )
,-π,3.1415,2.010010001…(相邻两个1之间0的个数逐渐增加)中,无理数有( )
A. 1个 B. 2个 C. 3个 D. 4个
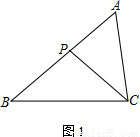
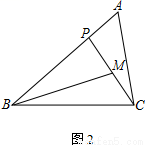
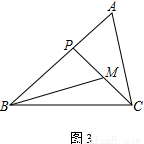
查看答案在△ABC中,P为边AB上一点.
(1)如图1,若∠ACP=∠B,求证:AC2=AP·AB;
(2)若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
如图,在Rt△ACB中,∠C=90°,AC=16cm,BC=8cm,动点P从点C出发,沿CA方向运动;动点Q同时从点B出发,沿BC方向运动,如果点P的运动速度为4cm/s,Q点的运动速度为2cm/s,那么运动几秒时,△ABC和△PCQ相似?
在宿州十一中校园文化艺术节中,九年级十班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.

解方程:x+5=x2-25.
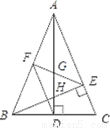
查看答案如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=4S△ADF.其中正确的有___________.
AE2;④S△ABC=4S△ADF.其中正确的有___________.
如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=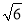 ,AD=2.当AB=_______时,△ABC与△ACD相似.
,AD=2.当AB=_______时,△ABC与△ACD相似.
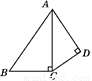
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 _______
设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=__.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为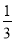 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )
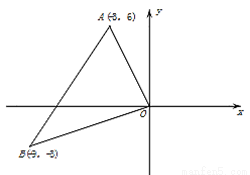
A. (-1,2) B. (-1,2)或(1,-2)
C. (-9,18)或(9,-18) D. (1,-2)
B 【解析】试题解析:∵点A(-3,6),以原点O为位似中心,相似比为,把△ABO缩小, ∴点A的对应点A′的坐标是(-1,2)或(1,-2), 故选B. 点睛:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
查看答案关于x的方程x2+kx﹣1=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
查看答案如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )
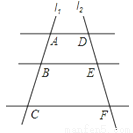
A. 4 B. 5 C. 6 D. 8
查看答案砀山果园场2015年水果产量为100吨,2017年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为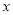 ,则根据题意可列方程为( )
,则根据题意可列方程为( )
A. 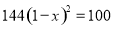 B.
B. 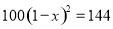
C. 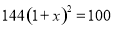 D.
D. 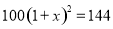
要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )
A. 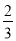 B.
B. 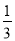 C.
C. 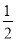 D.
D. 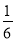
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
计算:
(1)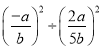 ·
·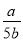
(2)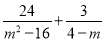
分解因式:
(1)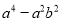
(2)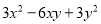
如图,在△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点,如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动,当点Q的运动速度为______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
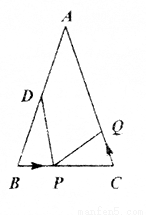
已知如图点D是△ABC的两外角平分线的交点,下列说法:
①AD=CD
②D到△ABC的三边所在直线的距离相等
③点D在∠B的平分线上
④若∠B=80°,则∠D=50°
其中正确的说法的序号是_____________________.
查看答案已知△ABC的两边长分别为AB=2和AC=6,第三边上的中线AD=x,则x的取值范围是______________.
查看答案当k=_______时,关于x的方程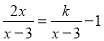 会产生增根.
会产生增根.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图示,数轴上点A所表示的数的绝对值为( )
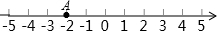
A.2 B.﹣2 C.±2 D.以上均不对
A 【解析】 试题分析:由数轴可得, 点A表示的数是﹣2,|﹣2|=2, 故选A. 考点:数轴;绝对值.在数﹣(﹣3),0,(﹣3)2,|﹣9|,﹣14中,正数的有( )个.
A. 2 B. 3 C. 4 D. 5
查看答案﹣ 的相反数是( )
的相反数是( )
A. ﹣5 B. 5 C. ﹣ D.
D. 
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
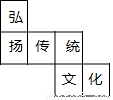
A. 传 B. 统 C. 文 D. 化
查看答案某公司有A产品40件,B产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润 (元) 如下表所示:
A产品的利润/元 | B产品的利润/元 | |
甲店 | 200 | 170 |
乙店 | 160 | 150 |
(1) 设分配给甲店A产品x件,这家公司卖出这100件产品的总利润为W (元),求W关于x的函数关系式,并求出x的取值范围;
(2) 若要求总利润不低于17560元;有多少种不同的分配方案? 并将各种方案设计出来;
(3) 为了促销,公司决定仅对甲店A产品让利销售,每件让利a元,但让利后A产品的每件利润仍高于甲店B产品的每件利润.甲店的B产品以及乙店的A,B产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
查看答案甲乙两人在同一条道路上同时出发,同时行进,甲步行,乙骑车,出发时甲在前,乙在后,图中l甲,l乙,分别表示出发后甲、乙离出发地的路程s(km)和经历的时间t(h)的关系.
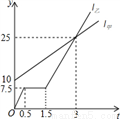
(1)乙出发时甲、乙相距___km.
(2)乙骑行一段路后,自行车发生故障,进行修理,所用的时间是___h.
(3)图象l甲,l乙相交的实际意义是什么?
(4)若乙的自行车没有故障,保持出发时的速度前进,求甲,乙相遇的时间和地点.
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

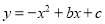 经过点A(3,0),B(﹣1,0).
经过点A(3,0),B(﹣1,0).