题目内容
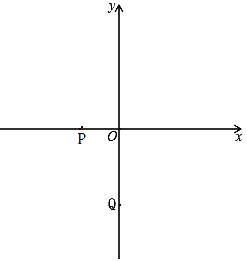
【题目】如图，已知：P（-1，0），Q（0，-2）.
（1）求直线PQ的函数解析式；
（2）如果M（0，
）是线段OQ上一动点，抛物线
经过点M和点P，
①求抛物线
与
轴另一交点N的坐标（用含
，的代数式表示）；
②若PN=
是，抛物线有最大值+1，求此时的值；
③若抛物线与直线PQ始终都有两个公共点，求的取值范围.
【答案】（1）
；（2）①N（
，0）；②
或
；③详见解析．
【解析】
(1)利用待定系数法求一次函数关系式即可;
(2) ①由抛物线
经过点M和点P可把点M和点P代入,再利用因式分解法变形可求得结果;
②
分两种情况,一种点N在点P的左侧,另一种在右侧,分别代入可求出;
③联立抛物线解析式和直线PQ的解析式,得到关于x的方程,根据“始终都有两个公共点”得
＞0，求出a的范围.
解：（1）设直线PQ的函数解析式为y=kx+b,把P（-1，0），Q（0，-2）代入得
,解得
,
∴
，
（2）①y=ax2+bx+ c 过M（0，m）和P（-1，0），
则
过P（-1，0）
∴
，
∴
∴
∴N（
，0）
②M（0，m），
，抛物线y=ax2+bx+c有最大值
，
（
，
）
当时，分两种情况，
（I）
解得：
，
（经验证，均成立）
（II）
，解得：
，
（经验证，均成立）
∴或
③
得
，
∵，
∴当
或
时，始终为正，
即抛物线y=ax2+bx+c与直线PQ始终都有两个公共点．
练习册系列答案
相关题目
