题目内容
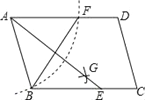
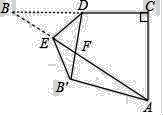
【题目】如图，在
中，
. 将线段
绕点
逆时针旋转
得到线段
，
是边
上的一动点，连接
交
于点
，连接
.
（1）求证：
；
（2）点
在边上，且
，连接
交于点
.
①判断与的位置关系，并证明你的结论；②连接
，若
，请直接写出线段长度的最小值.
【答案】（1）见解析；（2）①
,见解析；②
，见解析.
【解析】
（1）根据旋转的性质易得：AB=AD，∠BAF=∠DAF，结合AF=AF可证
即可得出结论；
（2）①在
上取
，连接
交
于点
，延长交
于点
，易证四边形
是正方形；通过证明
得
，由
知
，易证
.再证明
即可；
②根据当点
运动过程中，始终成立，点的轨迹在以
为直径的圆上求解即可.
（1）证明：∵
∴
∵
∴
在
和
中，
,
∴ （
）
∴
；
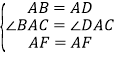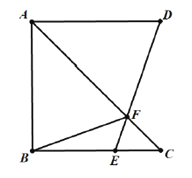
（2）①证明：在上取，连接交于点，延长交于点
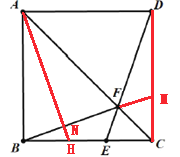
由（1）得∠DAC=∠DCA，AD=AB=BC，
∵
，
∴四边形是平行四边形
∵
∴四边形是正方形
∵ BH=CE，AB=DC，
∴ （）
∴
∵ （）
∴
∴
即
∵在
中，
∴
∴
即
②
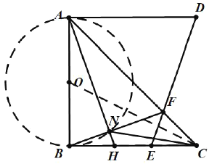
理由：由第二问可知，当点运动过程中， 始终成立，点的轨迹在以为直径的圆上，
与圆的交点即为最小值
.
练习册系列答案
轻松暑假总复习系列答案
相关题目
【题目】某商场经营某种品牌的玩具，购进时的单价是40元，根据市场调查：在一段时间内，销售单价是50元时，销售量是600件，而销售单价每涨2元，就会少售出20件玩具．
（1）不妨设该种品牌玩具的销售单价为x元（x＞50），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元，并把结果填写在表格中：
销售单价（元） | x |
销售量y（件） | ① |
销售玩具获得利润ω（元） | ② |
（2）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于54元，且商场要完成不少于400件的销售任务，求商场销售该品牌玩具获得的最大利润是多少元？
