题目内容
7.关于x的方程x2+mx+m=0的两个根的平方和为3,求m的值.分析 设方程两根为a、b,根据根与系数的关系得到a+b=-m,ab=m,由于a2+b2=3,利用完全平方公式变形得到(a+b)2-2ab=3,所以m2-2m-3=0,解得m1=3,m2=-1,然后根据根的判别式确定满足条件的m的值.
解答 解:设方程两根为a、b,
根据题意得a+b=-m,ab=m,
∵a2+b2=3,
∴(a+b)2-2ab=3,
∴m2-2m-3=0,解得m1=3,m2=-1,
当m=3时,原方程化为x2+3x+3=0,△=9-3×4<0,方程没有实数解,
∴m的值为-1.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.观察下列一组图形中点的个数的规律,第6个图中点的个数是( )

| A. | 31 | B. | 46 | C. | 51 | D. | 64 |
15.把多项式4a3-8a2b+4ab2分解因式,结果正确的是( )
| A. | a(2a+b)(a-2b) | B. | 4a(a2-2ab+b2) | C. | a(2a-b)2 | D. | 4a(a-b)2 |
19. 含有30°角的三角板如图放置在平面内,若三角板的最长边与直线m平行,则∠α的度数为( )
含有30°角的三角板如图放置在平面内,若三角板的最长边与直线m平行,则∠α的度数为( )
 含有30°角的三角板如图放置在平面内,若三角板的最长边与直线m平行,则∠α的度数为( )
含有30°角的三角板如图放置在平面内,若三角板的最长边与直线m平行,则∠α的度数为( )| A. | 20° | B. | 45° | C. | 60° | D. | 90° |
 如图,在△ABC中,∠C=90°,AB的中垂线交AB于点D,交BC于点E,连接AE,若∠BED=70°,则∠CAE的度数为50°.
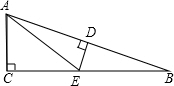
如图,在△ABC中,∠C=90°,AB的中垂线交AB于点D,交BC于点E,连接AE,若∠BED=70°,则∠CAE的度数为50°. 如图,△ABC中,∠C=90°,CD=15cm,BD=25cm,AC=30cm,求证:∠1=∠2.
如图,△ABC中,∠C=90°,CD=15cm,BD=25cm,AC=30cm,求证:∠1=∠2. 如图,在直角坐标系中,矩形ABCD的顶点A坐标为(-1,0),顶点B的坐标为(0,-2),经过顶点C的双曲线y=$\frac{k}{x}$(k>0)与线段AD交于点E,且AE:DE=2:1,则k的值为( )
如图,在直角坐标系中,矩形ABCD的顶点A坐标为(-1,0),顶点B的坐标为(0,-2),经过顶点C的双曲线y=$\frac{k}{x}$(k>0)与线段AD交于点E,且AE:DE=2:1,则k的值为( ) 如图所示,正方形ABCD的边长为1,依次以A,B,C,D为圆心,以AD,BE,CF,DG为半径画扇形,求阴影部分的面积.
如图所示,正方形ABCD的边长为1,依次以A,B,C,D为圆心,以AD,BE,CF,DG为半径画扇形,求阴影部分的面积.