��Ŀ����
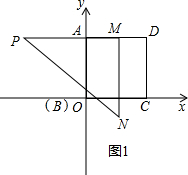
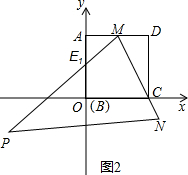
��ͼ��������ABCD�ı߳���2����BC��x���ϣ���AB��y���ϣ���һ�����dz���ͼ���ã�ͼ1��������MΪAD���е㣬��ʱ����ת���dzߣ���1�������dzߵ�һ�߾���C��ʱ����ʱ���dzߵ���һ�ߺ�AB�߽��ڵ�E1����ͼ2�������ʱֱ��PM�Ľ���ʽ��
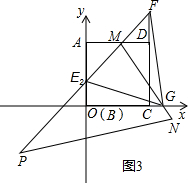
��2��������ת���dzߣ����dzߵ�һ����x�ύ�ڵ�G�����dzߵ���һ����AB����E2����ͼ3����PM���ӳ�����CD���ӳ��߽��ڵ�F����������GE2F�����Ϊ4�����ʱֱ��PM�Ľ���ʽ��
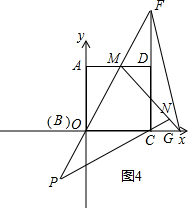
��3������ת�����dzߵ�һ�߾�����B����һֱ�DZߵ��ӳ�����x�ύ�ڵ�G����ͼ4�������ʱ������GOF�������
��������1��ͨ���������������������������PM��x��Ľ���G�����꣬M���������������Ȼ����ݴ���ϵ�������ֱ�ߵĽ���ʽ��
��2��ͨ��������������֤��������ȫ�ȵõ�E2F=GM�����������ε��������4���GM��ֵ���ٸ��ݹ��ɶ������AE2�ij���ȷ��E2�����꣬�����ݴ���ϵ������ֱ�ߵĽ���ʽ��
��3��ͨ��������������֤��������ȫ�ȵõ�OF=GM�����ù��ɶ���OM��ֵ������������ȫ�����OF��ֵ���Ӷ���������εĵ���ߣ��Ӷ���⣮
��2��ͨ��������������֤��������ȫ�ȵõ�E2F=GM�����������ε��������4���GM��ֵ���ٸ��ݹ��ɶ������AE2�ij���ȷ��E2�����꣬�����ݴ���ϵ������ֱ�ߵĽ���ʽ��
��3��ͨ��������������֤��������ȫ�ȵõ�OF=GM�����ù��ɶ���OM��ֵ������������ȫ�����OF��ֵ���Ӷ���������εĵ���ߣ��Ӷ���⣮
��� �⣺��1������M��MH��x���ڵ�H����PM��x���ڵ�G��
�⣺��1������M��MH��x���ڵ�H����PM��x���ڵ�G��
���MHG=90�㣬MH=CD
���ı���ABCD��������
���D=90�㣬AD=CD=2
���MHG=��D
��M��AD���е�
��MD=
AD=1��M��1��2��
����ת��֪��AMG=��HMC
�ߡ�HMC=��MCD
�ߡ�AMG=��MGC
���MGC=��MCD
���GHM�ס�CDM
��
=
��
=
��GH=4
��GB=3
��G��-3��0��
��ֱ��PM�Ľ���ʽΪ��y=kx+b���������
��ã�
��ֱ��PM�Ľ���ʽΪ��y=
x+
��2����FQ��AB��Q��RG��BG��G��AD���ӳ����ڵ�R��
��QF=GR����FQA=��R=90��
�ߡ�PMN=90��
���AE2M=��RMG
���FQE2�ա�GRM
��E2F=MG
��S��FE2G=4
��
E2F•MG=4
��E2F=2
��
�ߡ�AE2M�ա�DFM
��E2M=FM
��E2M=
����AM=1���ɹ��ɶ����ã�
AE2=1
��E2��0��1��
��PM�Ľ���ʽΪ��y=kx+b������ã�
��ã�
��ֱ�ߵĽ���ʽΪy=x+1
��3������F��FH��AO��H��GT��OC��G����AD���ӳ����ڵ�T
���FHO�ա�GTM
��FO=GM
��AM=1��AO=2���ɹ��ɶ����ã�
OM=
�ߡ�AMO�ա�DMF
��MF=OM
��OF=2
��GM=2
��S��GOF=
��2
��2
=10
��������GOF�����Ϊ10
 �⣺��1������M��MH��x���ڵ�H����PM��x���ڵ�G��
�⣺��1������M��MH��x���ڵ�H����PM��x���ڵ�G�����MHG=90�㣬MH=CD
���ı���ABCD��������
���D=90�㣬AD=CD=2
���MHG=��D
��M��AD���е�
��MD=
| 1 |
| 2 |
����ת��֪��AMG=��HMC
�ߡ�HMC=��MCD
�ߡ�AMG=��MGC
���MGC=��MCD
���GHM�ס�CDM
��
| GH |
| CD |
| HM |
| MD |
��
| GH |
| 2 |
| 2 |
| 1 |
��GH=4
��GB=3
��G��-3��0��
��ֱ��PM�Ľ���ʽΪ��y=kx+b���������
|
|
��ֱ��PM�Ľ���ʽΪ��y=
| 1 |
| 2 |
| 3 |
| 2 |
��2����FQ��AB��Q��RG��BG��G��AD���ӳ����ڵ�R��
��QF=GR����FQA=��R=90��
�ߡ�PMN=90��
���AE2M=��RMG
���FQE2�ա�GRM
��E2F=MG

��S��FE2G=4
��
| 1 |
| 2 |
��E2F=2
| 2 |
�ߡ�AE2M�ա�DFM
��E2M=FM
��E2M=
| 2 |
AE2=1
��E2��0��1��
��PM�Ľ���ʽΪ��y=kx+b������ã�
|
��ã�
|
��ֱ�ߵĽ���ʽΪy=x+1
��3������F��FH��AO��H��GT��OC��G����AD���ӳ����ڵ�T

���FHO�ա�GTM
��FO=GM
��AM=1��AO=2���ɹ��ɶ����ã�
OM=
| 5 |
�ߡ�AMO�ա�DMF
��MF=OM
��OF=2
| 5 |
��GM=2
| 5 |
��S��GOF=
| 1 |
| 2 |
| 5 |
| 5 |
��������GOF�����Ϊ10
������������һ��һ�κ������ۺ����⣬������ȫ�������ε����á����������ε����ã����ɶ��������ã����ô���ϵ���������Ľ���ʽ���Լ������������ʽ�����ã������ѶȽϴ�ѧ�����ۺ���������Ҫ��ϸߣ�

��ϰ��ϵ�д�
�����Ŀ
 19����ͼ��������ABCD��M���߶�BC��һ�㣬�Ҳ���B��C�غϣ�AE��DM��E��CF��DM��F����֤��AE2+CF2=AD2��
19����ͼ��������ABCD��M���߶�BC��һ�㣬�Ҳ���B��C�غϣ�AE��DM��E��CF��DM��F����֤��AE2+CF2=AD2�� ��ͼ��������ABCD�У�E����BC�ϣ�AEƽ�֡�BAC����BE=
��ͼ��������ABCD�У�E����BC�ϣ�AEƽ�֡�BAC����BE= ��ͼ��������ABCD�У�AB=6����E�ڱ�CD�ϣ���CD=3DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF�����н��ۣ��١�ABG�ա�AFG����BG=GC����AG��CF����S��FGC=3��������ȷ���۵ĸ����ǣ�������
��ͼ��������ABCD�У�AB=6����E�ڱ�CD�ϣ���CD=3DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF�����н��ۣ��١�ABG�ա�AFG����BG=GC����AG��CF����S��FGC=3��������ȷ���۵ĸ����ǣ������� 17����ͼ��������ABCD�ı߳�Ϊ4����һ���㹻���ֱ�����ǰ��ֱ�Ƕ�����ڵ�A���������ǰ������ֱ�DZ���CD���ڵ�F����CB�ӳ��߽��ڵ�E���ı���AECF�������
17����ͼ��������ABCD�ı߳�Ϊ4����һ���㹻���ֱ�����ǰ��ֱ�Ƕ�����ڵ�A���������ǰ������ֱ�DZ���CD���ڵ�F����CB�ӳ��߽��ڵ�E���ı���AECF������� ��ͼ��������ABCD�ı�CD��������ECGF�ı�CE�ϣ�����BE��DG��
��ͼ��������ABCD�ı�CD��������ECGF�ı�CE�ϣ�����BE��DG��