题目内容
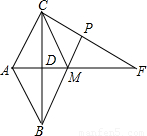
如图,AF垂直平分BC于D,∠ACB=∠F=30°,AC=4cm,点M从点D出发以每秒1cm的速度向终点F 运动,设运动时间为t,△CMF的面积为S.
运动,设运动时间为t,△CMF的面积为S.
(1)求S与t之间的函数关系;
(2)连接BM,并延长交CF于P,当S=4 时,判断△CMP的形状.
时,判断△CMP的形状.
解:(1)∵∠ACB=∠F=30°,AC=4cm,
∴AD=2,CD=BD=2 ,DF=6cm,
,DF=6cm,
∴S= CD•DF-
CD•DF- CD•DM=
CD•DM= ×2
×2 (6-t)=6
(6-t)=6 -
- t;
t;
(2)当S=4 时,6
时,6 -
- t=4
t=4 ,
,
解得t=2,
∴CM=FM=2,
∴△CMP是等腰三角形.
分析:(1)根据∠ACB=∠F=30°,AC=4cm求得CD=2 ,DF=6,则用三角形CDF的面积减去三角形CDM的面积即可得到s;
,DF=6,则用三角形CDF的面积减去三角形CDM的面积即可得到s;
(2)将S=4 代入求得的解析式即可求得DM的长,然后可以判断三角形CMP的形状.
代入求得的解析式即可求得DM的长,然后可以判断三角形CMP的形状.
点评:本题考查了三角形的面积、等腰三角形的判定等形状,与函数的知识结合起来考查是中考的热点.
∴AD=2,CD=BD=2
 ,DF=6cm,
,DF=6cm,∴S=
 CD•DF-
CD•DF- CD•DM=
CD•DM= ×2
×2 (6-t)=6
(6-t)=6 -
- t;
t;(2)当S=4
 时,6
时,6 -
- t=4
t=4 ,
,解得t=2,
∴CM=FM=2,
∴△CMP是等腰三角形.
分析:(1)根据∠ACB=∠F=30°,AC=4cm求得CD=2
 ,DF=6,则用三角形CDF的面积减去三角形CDM的面积即可得到s;
,DF=6,则用三角形CDF的面积减去三角形CDM的面积即可得到s;(2)将S=4
 代入求得的解析式即可求得DM的长,然后可以判断三角形CMP的形状.
代入求得的解析式即可求得DM的长,然后可以判断三角形CMP的形状.点评:本题考查了三角形的面积、等腰三角形的判定等形状,与函数的知识结合起来考查是中考的热点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
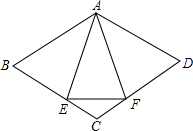 已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,BE=DF.
已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,BE=DF. 运动,设运动时间为t,△CMF的面积为S.
运动,设运动时间为t,△CMF的面积为S.
 时,判断△CMP的形状.
时,判断△CMP的形状.