Question

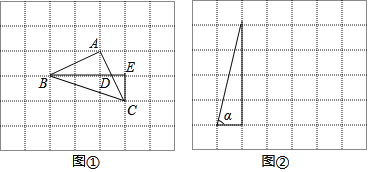
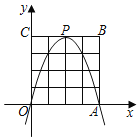
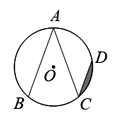
【题目】如图，点A，B，C，D在⊙O上，AB=AC，∠A=40°，CD∥AB，若⊙O的半径为2，则图中阴影部分的面积是(　　)

A.B.C.D.

Answer 1

【答案】B

【解析】

连接BC、OD、OC、BD，过O点作OE⊥CD于E点，先证△COD是等边三角形，再根据阴影部分的面积是S扇形COD-S△COD计算可得．

如图所示，连接BC、OD、OC、BD，过O点作OE⊥CD于E点，

∵∠A=40°，AB=AC，
∴∠ABC=70°，
∵CD∥AB，
∴∠ACD=∠A=40°，
∴∠ABD=∠ACD=40°，
∴∠DBC=30°，
则∠COD=2∠DBC=60°，
又OD=OC，
∴△COD是等边三角形，

∴OD=CD=2，DE=

∴
则图中阴影部分的面积是S扇形COD-S△COD
故选：B．