题目内容
17.先化简,再求值:$\frac{{x}^{2}-4x+4}{{x}^{2}-2x}$÷(x-$\frac{4}{x}$),其中x=4-2sin30°.分析 先通分,再把除法转化成乘法,然后约分,最后求出x的值,再把它代入原式,进行计算即可.
解答 解:$\frac{{x}^{2}-4x+4}{{x}^{2}-2x}$÷(x-$\frac{4}{x}$)
=$\frac{(x-2)2}{x(x-2)}$÷$\frac{x2-4}{x}$
=$\frac{(x-2)2}{x(x-2)}$×$\frac{x}{(x+2)(x-2)}$
=$\frac{1}{x+2}$,
当x=4-2sin30°=3时,
原式=$\frac{1}{3+2}$=$\frac{1}{5}$.
点评 此题考查了分式的化简求值,用到的知识点是分式的化简步骤和特殊角的三角函数值,关键是把分式化到最简,然后代值计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.我市为了增强学生的体质,组织了一次排球联赛,赛制为单循环形式(每两队之间都赛一场),共进行了15场比赛,则参加比赛的球队共有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 5个或6个 |
2.甲、乙两个水泥厂向A、B两个建筑工地运送水泥.已知甲地可调出100吨水泥,乙地可调出70吨水泥;A建筑工地需80吨水泥,B建筑工地需90吨水泥;甲、乙两个水泥厂到A、B两个建筑工地的路程和运费如下表[运费(元/吨•千米)表示每吨货物运送1千米的费用]
(1)设甲水泥厂运往A建筑工地水泥x吨,求总运费y(元)关于x(吨)的函数关系式.
(2)如何调运才能使总运费最节省?最节省的总运费是多少.
| 路程(千米) | 运费(元/吨•千米) | |||
| 甲水泥厂 | 乙水泥厂 | 甲水泥厂 | 乙水泥厂 | |
| A建筑工地 | 20 | 15 | 12 | 12 |
| B建筑工地 | 25 | 20 | 10 | 8 |
(2)如何调运才能使总运费最节省?最节省的总运费是多少.
6.下列分式是最简分式的是( )
| A. | $\frac{1-x}{x-1}$ | B. | $\frac{x-1}{{x}^{2}-1}$ | C. | $\frac{2x}{{x}^{2}+1}$ | D. | $\frac{4}{2x}$ |
7.估计2$\sqrt{3}$的值在( )
| A. | 1和2之间 | B. | 2和3之间 | C. | 3和4之间 | D. | 4和5之间 |
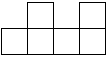
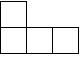
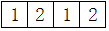 由若干个相同的小正方体搭成的一个几何体的俯视图如图所示,小正方形中的数字表示该位置的小正方体的个数,这个几何体的主视图是( )
由若干个相同的小正方体搭成的一个几何体的俯视图如图所示,小正方形中的数字表示该位置的小正方体的个数,这个几何体的主视图是( )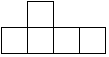
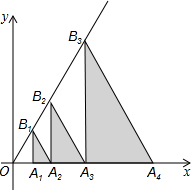 如图,△OB1A2、△OB2A3、△OB3A4、…△OBnAn+1都是等边三角形,其中B1A1、B2A2、…BnAn都与x轴垂直,点A1、A2、…An都在x轴上,点B1、B2、…Bn都在直线y=$\sqrt{3}$x上,已知OA1=1,则点A2016的坐标为(22015,0).
如图,△OB1A2、△OB2A3、△OB3A4、…△OBnAn+1都是等边三角形,其中B1A1、B2A2、…BnAn都与x轴垂直,点A1、A2、…An都在x轴上,点B1、B2、…Bn都在直线y=$\sqrt{3}$x上,已知OA1=1,则点A2016的坐标为(22015,0).