题目内容
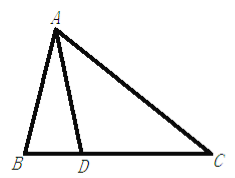
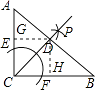
【题目】如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图: 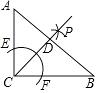
①以C为圆心,以适当长为半径画弧交AC于E,交BC于F.
②分别以E,F为圆心,以大于 ![]() EF的长为半径作弧,两弧相交于P;
EF的长为半径作弧,两弧相交于P;
③作射线CP交AB于点D,
若AC=3,BC=4,则△ACD的面积为 .
【答案】![]()
【解析】解:过点D作DG⊥AC,DH⊥BC,垂足分别为G、H,
∵由题意可知CP是∠ACB的平分线,
∴DG=DH.
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴S△ABC=S△ACD+S△BCD,即 ![]() ×3×4=
×3×4= ![]() ×3DG+
×3DG+ ![]() ×4DG,解得DG=
×4DG,解得DG= ![]() ,
,
∴△ACD的面积= ![]() ×3×
×3× ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】掌握勾股定理的概念是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目