题目内容
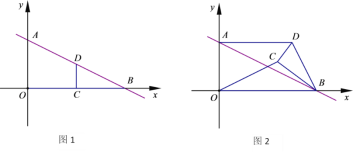
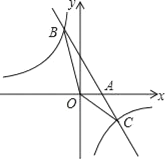
【题目】如图,点![]() 和点
和点![]() 是反比例函数
是反比例函数![]() 图象上的两点,一次函数
图象上的两点,一次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() .已知
.已知![]() 与
与![]() 的面积满足
的面积满足![]() .
.

(1)![]() = _____,
= _____,![]() = _____;
= _____;
(2)已知点![]() 在线段
在线段![]() 上,当
上,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)3,8;(2)![]() .
.
【解析】
(1)由一次函数解析式求得点B的坐标,易得OB的长度,结合点A的坐标和三角形面积公式求得S△OAB=3,所以S△ODE=4,由反比例函数系数k的几何意义求得m的值;
(2)利用待定系数法确定直线AC函数关系式,易得点C的坐标;利用∠PDE=∠CBO,∠COB=∠PED=90°判定△CBO∽△PDE,根据该相似三角形的对应边成比例求得PE、DE的长度,易得点D的坐标.
(1)由一次函数![]() 知,
知,![]() .
.
又点A的坐标是![]() ,
,
![]() .
.
![]() .
.
![]() .
.
∵点![]() 是反比例函数
是反比例函数![]() 图象上的点,
图象上的点,
![]() ,则
,则![]() .
.
(2)由(1)知,反比例函数解析式是![]() .
.
![]() ,即
,即![]() .
.
故![]() ,将其代入
,将其代入![]() 得到:
得到:![]() .
.
解得![]() .
.
∴直线![]() 的解析式是:
的解析式是:![]() .
.
令![]() ,则
,则![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
由(1)知,![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,即
,即![]() ①,
①,
又![]() ②.
②.
联立①②,得![]() (舍去)或
(舍去)或![]() .
.
故![]() .
.


【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?