题目内容
 如图,已知点A的坐标为(
如图,已知点A的坐标为( ,3),AB⊥x轴,垂足为B,连接OA,反比例函数
,3),AB⊥x轴,垂足为B,连接OA,反比例函数 (k>0)的图象与线段OA,AB分别交与点C,D.若AB=3BD,则四边形BOCD的面积为________.
(k>0)的图象与线段OA,AB分别交与点C,D.若AB=3BD,则四边形BOCD的面积为________.
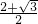
分析:连接CD,作CE⊥x轴于E,由于点A的坐标为(
 ,3),AB=3BD,D点坐标为(
,3),AB=3BD,D点坐标为( ,1),得到k=
,1),得到k= ,再利用待定系数法求出直线OA的解析式为y=
,再利用待定系数法求出直线OA的解析式为y= x,然后解方程组
x,然后解方程组 得C点坐标为(1,
得C点坐标为(1, ),再利用四边形BOCD的面积=S△OCD+S梯形CEBD进行计算即可.
),再利用四边形BOCD的面积=S△OCD+S梯形CEBD进行计算即可.解答:
 解:连接CD,作CE⊥x轴于E,如图
解:连接CD,作CE⊥x轴于E,如图∵点A的坐标为(
 ,3),AB=3BD,
,3),AB=3BD,∴D点坐标为(
 ,1),
,1),∴k=
 ×1=
×1=
设直线OA的解析式为y=kx,把A(
 ,3)代入得3=
,3)代入得3= k,解得k=
k,解得k= ,
,∴直线OA的解析式为y=
 x,
x,解方程组
 得
得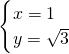 或
或 ,
,∴C点坐标为(1,
 ),
),∴四边形BOCD的面积=S△OCE+S梯形CEBD=
 +
+ (1+
(1+ )×(
)×( -1)=
-1)=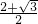 .
.故答案为:
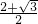 .
.点评:本题考查了反比例函数y=
 (k≠0)的k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|.
(k≠0)的k的几何意义:过反比例函数图象上任意一点分别作x轴、y轴的垂线,则垂线与坐标轴所围成的矩形的面积为|k|. 
练习册系列答案
相关题目
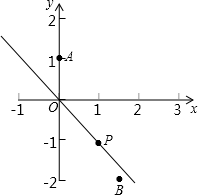 如图,已知点A的坐标为(0,1),点B的坐标为(
如图,已知点A的坐标为(0,1),点B的坐标为(| 3 |
| 2 |
| A、(2,-2) | ||||
| B、(4,-4) | ||||
C、(
| ||||
| D、(5,-5) |
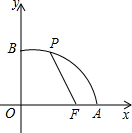 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-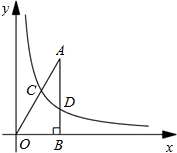 如图,已知点A的坐标为(
如图,已知点A的坐标为(

 如图,已知点A的坐标为(
如图,已知点A的坐标为(