题目内容
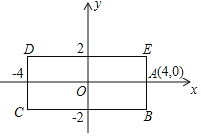
【题目】如图，在平面直角坐标系
中，已知
，将线段
平移至
，点
在
轴正半轴上，
，且
．连接
，
，
，
．
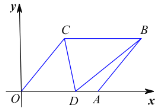
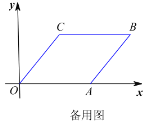
（1）写出点
的坐标为 ；点
的坐标为 ；
（2）当
的面积是
的面积的3倍时，求点的坐标；
（3）设
，
，
，判断
、
、
之间的数量关系，并说明理由．
【答案】（1）
，
；（2）点D的坐标为
或
；（3）
之间的数量关系
，或
，理由见解析．
【解析】
（1）由二次根式成立的条件可得a和b的值，由平移的性质确定BC∥OA，且BC=OA，可得结论；
（2）分点D在线段OA和在OA延长线两种情况进行计算；
（3）分点D在线段OA上时，α+β=θ和在OA延长线α-β=θ两种情况进行计算；
解：（1）∵
，
∴a=2，b=3，
∴点C的坐标为（2，3），
∵A（4，0），
∴OA=BC=4，
由平移得：BC∥x轴，
∴B（6，3），
故答案为：，；
（2）设点D的坐标为
∵△ODC的面积是△ABD的面积的3倍
∴
∴
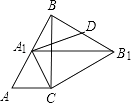
①如图1，当点D在线段OA上时，
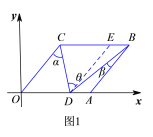
由，得
解得
∴点D的坐标为
②如图2，当点D在OA得延长线上时，
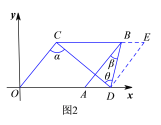
由，得
解得
∴点D的坐标为
综上，点D的坐标为或．
（3）①如图1，当点D在线段OA上时，
过点D作DE∥AB，与CB交于点E
．由平移知OC∥AB，∴DE∥OC
∴
又
∴．
②如图2，当点D在OA得延长线上时，
过点D作DE∥AB，与CB得延长线交于点E
由平移知OC∥AB，∴DE∥OC
∴
又
∴．
综上，之间的数量关系，或．
练习册系列答案
阅读快车系列答案
相关题目
