题目内容
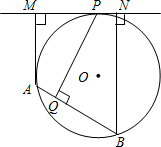 如图,MN切⊙O于P,AB是⊙O的弦,AM⊥MN于M,BN⊥MN于N,PQ⊥AB于Q.
如图,MN切⊙O于P,AB是⊙O的弦,AM⊥MN于M,BN⊥MN于N,PQ⊥AB于Q.
求证:PQ2=AM•BN.
 证明:连接AP,BP,
证明:连接AP,BP,∵AM⊥MN于M,PQ⊥AB于Q.
∴∠AMP=∠PQB=90°,
∵∠1=∠2,
∴△PAM∽△BPQ,
∴
 ,
,同理可得:
 ,
,∴
 ,
,∴PQ2=AM•BN.
分析:连接AP,BP欲证题中结论,只需证
 ,而要证此式,必须借助于第三个比即中间比.由△PAM∽△BPQ可得
,而要证此式,必须借助于第三个比即中间比.由△PAM∽△BPQ可得 ,再由△PBN∽△APQ可得
,再由△PBN∽△APQ可得 ,进而证明PQ2=AM•BN.
,进而证明PQ2=AM•BN.点评:本题考查了和圆有关的比例线段的证明题,可由所要证的比例式找到相似三角形;当要证明的比例式不能直接应用有关定理和相似三角形来证明时,可以考虑等量代换.等量代换通常有等线段代换、等比代换等.

练习册系列答案
相关题目
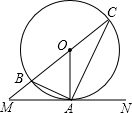 如图,MN切⊙O于A点,AC为弦,BC为直径,那么下列命题中假命题是( )
如图,MN切⊙O于A点,AC为弦,BC为直径,那么下列命题中假命题是( )| A、∠MAB和∠ABC互余 | ||
| B、∠CAN=∠ABC | ||
C、OA=
| ||
| D、MA2=MB•BC |
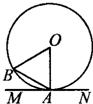 16、如图,MN切⊙O于点A,∠AOB=60°,那么∠BAM等于( )
16、如图,MN切⊙O于点A,∠AOB=60°,那么∠BAM等于( ) (2004•呼和浩特)如图,MN切⊙O于P,AB是⊙O的弦,AM⊥MN于M,BN⊥MN于N,PQ⊥AB于Q.
(2004•呼和浩特)如图,MN切⊙O于P,AB是⊙O的弦,AM⊥MN于M,BN⊥MN于N,PQ⊥AB于Q. 如图,MN切⊙O于A点,AC为弦,BC为直径,∠CAN=65°,则∠BMA的度数为
如图,MN切⊙O于A点,AC为弦,BC为直径,∠CAN=65°,则∠BMA的度数为