题目内容
同圆的内接正三角形与正六边形的边长之比为（ ）
A．1：2 B．1：1 C．
：1 D．2：1
C．
【解析】
试题分析：设圆的半径为R，如图（一）， 连接OB，过O作OD⊥BC于D，
则∠OBC=30°，BD=OB•cos30°=
R，
故BC=2BD=
R；
如图（二），连接OA、OB，过O作OG⊥AB，
则△OAB是等边三角形，
故AG=OA•cos60°=
R，AB=2AG=R，
∴圆内接正三角形、正六边形的边长之比为R：R=：1．
故选C．
考点：正多边形和圆．
练习册系列答案
相关题目
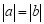，则a与b的关系是（ ）
经过点A（3，0），B（－1，0）．
，…，它们是按一定规律排列的，那么这一组数的第n个数是 ．