题目内容
已知方程: ,那么x2+3x= .
,那么x2+3x= .
【答案】分析:本题考查用换元法解分式方程的能力,可根据方程特点设y=x2+3x,将原方程可化简为关于y的方程.
解答:解:设y=x2+3x,则 -y=2;
-y=2;
两边同乘以y可得y2+2y-3=0,
解得y1=1或y2=-3,
即x2+3x=1或x2+3x=-3;
故答案为1或-3.
点评:本题主要考查换元法解分式方程,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化.属于基础题.
解答:解:设y=x2+3x,则
 -y=2;
-y=2;两边同乘以y可得y2+2y-3=0,
解得y1=1或y2=-3,
即x2+3x=1或x2+3x=-3;
故答案为1或-3.
点评:本题主要考查换元法解分式方程,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化.属于基础题.

练习册系列答案
相关题目
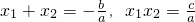 .根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______.
.根据这一性质,我们可以求出已知方程关于x1,x2的代数式的值.例如:已知x1,x2为方程x2-2x-1=0的两根,则x1+x2=______,x1•x2=______.那么x12+x22=(x1+x2)2-2x1x2=______. 的值.
的值. .∴
.∴
 .
. 是方程x2-x-1=0的两根.∴
是方程x2-x-1=0的两根.∴ .∴
.∴ 的值.
的值. ,那么x2+3x=________.
,那么x2+3x=________.