题目内容
（2007•荆州）如图直角三角板ABC中，∠A=30°，BC=3cm，将直角三角板ABC绕着直角顶点C顺时针方向旋转90°至△A1B1C1的位置，再沿CB向左平移使点B1落在△ABC的斜边AB上，点A1平移到点A2的位置，则点A?A1?A2运动的路径长度是 cm．（结果用带π和根号的式子表示）
【答案】分析：点A由A?A1?A2运动的路程先是一段弧，然后是一直线，所以根据弧长公式可得．
解答：
解：根据勾股定理可得：AC=3
移动距离为
+A1A2
∵∠A=30°，BC=3cm
∴AB=6
利用相似三角形可得
=
解得A1A2=
-
填
+
-
．
点评：本题主要是根据弧长公式先求出那段弧长，再根据三角形的相似求出B1B2的长即可．
解答：
解：根据勾股定理可得：AC=3移动距离为
+A1A2∵∠A=30°，BC=3cm
∴AB=6
利用相似三角形可得
=解得A1A2=
-填
+-．点评：本题主要是根据弧长公式先求出那段弧长，再根据三角形的相似求出B1B2的长即可．
练习册系列答案
阅读快车系列答案
相关题目
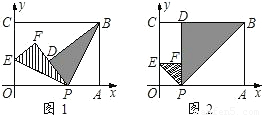
（k＜0）图象上一点，过D作DC⊥y轴于C，DE⊥x轴于E，一次函数y=-x+m与y=-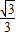
x+2的图象都过C点，与x轴分别交于A、B两点．若梯形DCAE的面积为4，求k的值．
（k＜0）图象上一点，过D作DC⊥y轴于C，DE⊥x轴于E，一次函数y=-x+m与y=-
x+2的图象都过C点，与x轴分别交于A、B两点．若梯形DCAE的面积为4，求k的值．
