题目内容
如图(1),正方形ABCD的边长为8,点M、N分别为边AD、BC的中点.现有动点E沿N→B→A以每秒1个单位的速度运动,同时动点F沿C→D→M以相同速度运动.(1)求在运动过程中形成的△CEF的面积S与运动的时间t之间的函数关系,并写出自变量t的取值范围;
(2)何时点E、F与正方形的某一个顶点恰好连成一个等腰三角形,请写出此时t的值;
(3)如图(2),当点F从C向D运动时,连接FN,作FN的垂线交直线DA于点G,点P为GN的中点,连接PM、MF、PF.当△PMF的面积为12时,求对应的t的值.

【答案】分析:(1)分三种情况:当0≤t≤4时;当4≤t≤8时;当8≤t≤12时;根据图形的面积公式得出△CEF的面积S与运动的时间t之间的函数关系;
(2)分三种情况:当0≤t≤4时;当4≤t≤8时;当8≤t≤12时;根据等腰三角形的性质即可求得t的值;
(3)先根据S△PMF=S矩形MNCD+S△PMN-S△NCF-S△MDF-S△PNF列出代数式,再根据△PMF的面积为12,求对应的t值.
解答:解:(1)当0≤t≤4时, ;
;
当4<t≤8时,S=4t;
当8<t≤12时, .
.
(2)当0≤t≤4时,当t= 时,EF=DF;当t=4时,EF=AF;
时,EF=DF;当t=4时,EF=AF;
当4<t≤8时,当t=8时,EF=EC;
当8<t≤12时,当t= 时,EF=FC;当t=
时,EF=FC;当t= 时,EF=EB;
时,EF=EB;
∴t= 或4或8或
或4或8或 或
或 .
.
(3)S△PMF=S矩形MNCD+S△PMN-S△NCF-S△MDF-S△PNF
=
= ,
,
令 =12,
=12,
解得t= .
.
点评:考查了相似形综合题,涉及到图形的面积计算,等腰三角形的性质,函数思想好分类思想,(3)也可利用S△PMF=S△PMN+S△FMN-S△PNF来计算.
(2)分三种情况:当0≤t≤4时;当4≤t≤8时;当8≤t≤12时;根据等腰三角形的性质即可求得t的值;
(3)先根据S△PMF=S矩形MNCD+S△PMN-S△NCF-S△MDF-S△PNF列出代数式,再根据△PMF的面积为12,求对应的t值.
解答:解:(1)当0≤t≤4时,
 ;
;当4<t≤8时,S=4t;
当8<t≤12时,
 .
.(2)当0≤t≤4时,当t=
 时,EF=DF;当t=4时,EF=AF;
时,EF=DF;当t=4时,EF=AF;当4<t≤8时,当t=8时,EF=EC;
当8<t≤12时,当t=
 时,EF=FC;当t=
时,EF=FC;当t= 时,EF=EB;
时,EF=EB;∴t=
 或4或8或
或4或8或 或
或 .
.(3)S△PMF=S矩形MNCD+S△PMN-S△NCF-S△MDF-S△PNF
=

=
 ,
,令
 =12,
=12,解得t=
 .
.点评:考查了相似形综合题,涉及到图形的面积计算,等腰三角形的性质,函数思想好分类思想,(3)也可利用S△PMF=S△PMN+S△FMN-S△PNF来计算.

练习册系列答案
相关题目
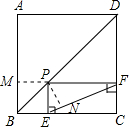 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF; ③△APD一定是等腰三角形; ④∠PFE=∠BAP;⑤PD=
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF.给出下列五个结论:①AP=EF;②AP⊥EF; ③△APD一定是等腰三角形; ④∠PFE=∠BAP;⑤PD= 15、如图,在四个正方形拼接成的图形中,以这个十个点中任意三点为顶点,共能组成
15、如图,在四个正方形拼接成的图形中,以这个十个点中任意三点为顶点,共能组成 18、如图,在3个正方形内分别填上适当的数使得折成正方体后相对面上的两个数互为相反数,则A、B、C依次为( )
18、如图,在3个正方形内分别填上适当的数使得折成正方体后相对面上的两个数互为相反数,则A、B、C依次为( ) (2012•柳州)如图,给出了正方形ABCD的面积的四个表达式,其中错误的是( )
(2012•柳州)如图,给出了正方形ABCD的面积的四个表达式,其中错误的是( )