题目内容
如图,将线段AB沿箭头方向平移2 cm得到线段CD,若AB=3 cm,则四边形ABDC的周长为( )
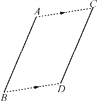
A. 8 cm B. 10 cm C. 12 cm D. 20 cm
练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
题目内容
如图,将线段AB沿箭头方向平移2 cm得到线段CD,若AB=3 cm,则四边形ABDC的周长为( )

A. 8 cm B. 10 cm C. 12 cm D. 20 cm
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案