题目内容
如图,甲建筑物的高AB为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.
 |
解:过点A作AE⊥CD于点E,
∵AB⊥BC,DC⊥BC,
∴四边形ABCE为矩形,
∴CE=AB=40m,
∵∠DAE=45°,
∴AE=ED,
设AE=DE=xm,则BC=xm,
在Rt△BCD中,
∵∠DBC=60°,
∴CD=BC•tan60°,
即40+x= x,
x,
解得:x=20( +1),
+1),
则CD的高度为:x+40=60+20 (m).
(m).
答:乙建筑物的高DC为(60+20 )m.
)m.


练习册系列答案
相关题目
下列计算正确的是( )
|
| A. | (﹣1)﹣1=1 | B. | (﹣1)0=0 | C. | |﹣1|=﹣1 | D. | ﹣(﹣1)2=﹣1 |
如图,在正方形ABCD中,对角线BD的长为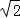 .若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为
.若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为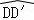 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )

|
| A. |
| B. |
| C. |
| D. | π﹣2 |
 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )

 的两个根分别是
的两个根分别是 、
、 ,且
,且 ,则k的值为___________.
,则k的值为___________. ﹣1
﹣1
 ﹣
﹣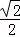 时,求点E的坐标;
时,求点E的坐标;
 的两根,且
的两根,且 ,若这两个圆相切,则
,若这两个圆相切,则 = .
= .