题目内容
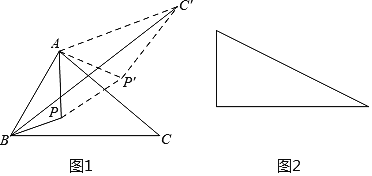
【题目】如图,![]() 中,
中,![]() ,
,![]() ,在以
,在以![]() 的中点
的中点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴建立的平面直角坐标系中,将
轴建立的平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 旋转至
旋转至![]() 轴的正半轴上的点
轴的正半轴上的点![]() 处,若
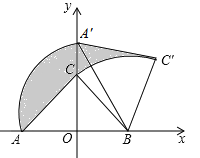
处,若![]() ,则图中阴影部分面积为________.
,则图中阴影部分面积为________.
【答案】![]()
【解析】
根据等腰直角三角形的性质求出AB,再根据旋转的性质可得A′B=AB,然后求出∠OA′B=30°,再根据直角三角形两锐角互余求出∠A′BA=60°,即旋转角为60°,再根据S阴影=S扇形ABA′+S△A′BC′-S△ABC-S扇形CBC′=S扇形ABA′-S扇形CBC′,然后利用扇形的面积公式列式计算即可得解.
解:∵∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴AB=2OA=2OB=4,BC=2![]() ,
,
∵△ABC绕点B顺时针旋转点A在A′处,
∴BA′=AB,
∴BA′=2OB,
∴∠OA′B=30°,
∴∠A′BA=60°,
即旋转角为60°,
S阴影=S扇形ABA′+S△A′BC′-S△ABC-S扇形CBC′,
=S扇形ABA′-S扇形CBC′,
= ![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,点
,点![]() 为射线
为射线![]() ,
,![]() 的交点.
的交点.
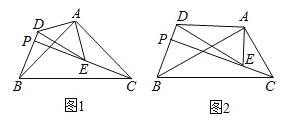
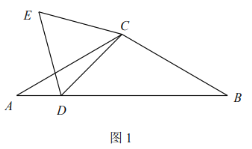
(1)问题提出:如图1,若![]() ,
,![]() .
.
①![]() 与
与![]() 的数量关系为________;
的数量关系为________;
②![]() 的度数为________.
的度数为________.
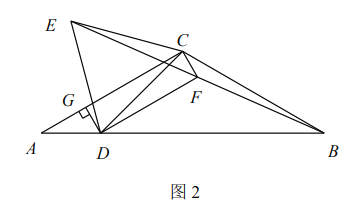
(2)猜想论证:如图2,若![]() ,则(1)中的结论是否成立?请说明理由.
,则(1)中的结论是否成立?请说明理由.