题目内容
【题目】已知：如图，菱形ABCD中，AB=10cm，BD=12cm，对角线AC与BD相交于点O，直线MN以1cm/s从点D出发，沿DB方向匀速运动，运动过程中始终保持MN⊥BD，垂足是点P，过点P作PQ⊥BC，交BC于点Q．（0＜t＜6）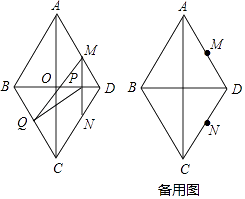 
（1）求线段PQ的长；（用含t的代数式表示）
（2）设△MQP的面积为y（单位：cm2），求y与t的函数关系式；
（3）是否存在某时刻t，使线段MQ恰好经过点O？若存在求出此时t的值；若不存在，请说明理由．
【答案】
（1）
解：如图1中，
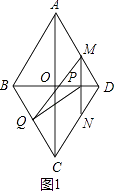
∵四边形ABCD是菱形，
∴BC=AB=10，OB=OD=6，BD⊥AC，
在Rt△BOC中，OC= 
= 
=8，
∴sin∠OBC= 
= 
，
在Rt△PBQ中，∵PB=12﹣t，
sin∠PBQ= 
= ，
∴PQ= （12﹣t）= 
﹣ t（0＜t＜6）
（2）
解：如图2中，作QH⊥MN于H．
∵∠QPH+∠BPQ=90°，∠BPQ+∠CBO=90°，
∴∠QPH=∠CBO，
∴QH=PQsin∠QPH= （ ﹣ t），
易知PM= 
t，
∴y= 
PMQH= t （ ﹣ t）= 
﹣ 
t（0＜t＜6）
（3）
解：如图3中，连接QN．
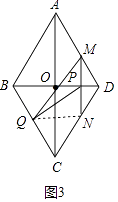
当MQ经过点O时，易证△BOQ≌△DOM，
∴BQ=DM，OM=OQ，
∵PM=PN，
∴OP∥QN，NQ=2OP，
∴QN⊥MN，QN= （ ﹣ t），
∴ （ ﹣ t）=2（6﹣t），
解得t= 
，
∴t= 时，MQ经过点O
【解析】【（1）如图1中，在Rt△BOC中，OC= = =8，推出sin∠OBC= = ，在Rt△PBQ中，由PB=12﹣t推出sin∠PBQ= = ，即可求出PQ．（2）如图2中，作QH⊥MN于H．求出QH、PM即可解决问题．（3）如图3中，连接QN只要证明QM经过点O时，OP是△MQN的中位线，得到QN=2OP，由此列出方程即可解决问题．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对相似三角形的应用的理解，了解测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解．
