题目内容
2.如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=2$\sqrt{3}$CM+$\frac{2\sqrt{3}}{3}$BN.

分析 (1)①通过角的计算找出∠ACD=∠BCE,再结合△ACB和△DCE均为等腰三角形可得出“AC=BC,DC=EC”,利用全等三角形的判定(SAS)即可证出△ACD≌△BCE,由此即可得出结论AD=BE;
②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC,再通过角的计算即可算出∠AEB的度数;
(2)根据等腰三角形的性质结合顶角的度数,即可得出底角的度数,利用(1)的结论,通过解直角三角形即可求出线段AD、DE的长度,二者相加即可证出结论.
解答 (1)①证明:∵∠CAB=∠CBA=∠CDE=∠CED=50°,
∴∠ACB=∠DCE=180°-2×50°=80°.
∵∠ACB=∠ACD+∠DCB,∠DCE=∠DCB+∠BCE,
∴∠ACD=∠BCE.
∵△ACB和△DCE均为等腰三角形,
∴AC=BC,DC=EC.
在△ACD和△BCE中,有$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=EC}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴AD=BE.
②解:∵△ACD≌△BCE,
∴∠ADC=∠BEC.
∵点A,D,E在同一直线上,且∠CDE=50°,
∴∠ADC=180°-∠CDE=130°,
∴∠BEC=130°.
∵∠BEC=∠CED+∠AEB,且∠CED=50°,
∴∠AEB=∠BEC-∠CED=130°-50°=80°.
(2)证明:∵△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=120°,
∴∠CDM=∠CEM=$\frac{1}{2}$×(180°-120°)=30°.
∵CM⊥DE,
∴∠CMD=90°,DM=EM.
在Rt△CMD中,∠CMD=90°,∠CDM=30°,
∴DE=2DM=2×$\frac{CM}{tan∠CDM}$=2$\sqrt{3}$CM.
∵∠BEC=∠ADC=180°-30°=150°,∠BEC=∠CEM+∠AEB,
∴∠AEB=∠BEC-∠CEM=150°-30°=120°,
∴∠BEN=180°-120°=60°.
在Rt△BNE中,∠BNE=90°,∠BEN=60°,
∴BE=$\frac{BN}{sin∠BEN}$=$\frac{2\sqrt{3}}{3}$BN.
∵AD=BE,AE=AD+DE,
∴AE=BE+DE=$\frac{2\sqrt{3}}{3}$BN+2$\sqrt{3}$CM.
点评 本题考查了等腰三角形的性质、全等三角形的判定及性质、解直角三角形以及角的计算,解题的关键是:(1)通过角的计算结合等腰三角形的性质证出△ACD≌△BCE;(2)找出线段AD、DE的长.本题属于中档题,难度不大,但稍显繁琐,解决该题型题目时,利用角的计算找出相等的角,再利用等腰三角形的性质找出相等的边或角,最后根据全等三角形的判定定理证出三角形全是关键.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案(1)把油箱加满油;
(2)记录了两次加油时的累计里程(注:“累计里程”指汽车从出厂开始累计行驶的路程),以下是张老师连续两次加油时的记录:
| 加油时间 | 加油量(升) | 加油时的累计里程(千米) |
| 2016年4月28日 | 18 | 6200 |
| 2016年5月16日 | 30 | 6600 |
| A. | 3升 | B. | 5升 | C. | 7.5升 | D. | 9升 |
| A. | a>0 | B. | a=0 | C. | c>0 | D. | c=0 |
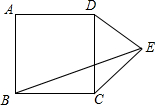 如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=$\frac{1}{3}$.
如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=$\frac{1}{3}$.