Question

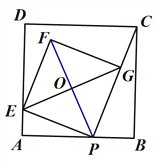
【题目】如图，已知正方形ABCD的边长为4，点P是AB边上的一个动点，连接CP，过点P作PC的垂线交AD于点E，以PE为边作正方形PEFG，顶点G在线段PC上. 对角线EG、FP相交于点O.

（1）若AP=3，求AE的长；

（2）连接AC，判断点O是否在AC上，并说明理由；

（3）在点P从点A到点B的运动过程中，正方形PEFG也随之运动，求DE的最小值．

Answer 1

【答案】（1）AE=；（2）见解析；（3）DE的最小值为3.

【解析】试题分析：

（1）由已知易证∠A=∠B=∠EPG=90°，由此可得∠AEP+∠APE=90°，∠BPC+∠APE=90°，从而可得∠AEP=∠BPC，这样可证得△APE∽△BCP，再由相似三角形的性质结合AB=BC=4，AP=3即可求得AE的长；

（2）过点O分别作AB、AD的垂线，垂足分别为M、N，由已知条件易证△OPM≌△OEN，可得OM=ON，由此可得点O在∠BAD的平分线上，由正方形的对角线平分一组对角可得AC是∠BAD的平分线，从而说明点O在AC上；

（3）设AP=x，则BP=4﹣x，由（1）可知：△APE∽△BCP，从而可得，即 ，解得：AE=x﹣x2=﹣（x﹣2）2+1，结合AE+DE=AD=4可得DE=（x﹣2）2+3，由此即可得到DE的最小值为3.

试题解析：

（1）∵四边形ABCD、四边形PEFG是正方形，

∴∠A=∠B=∠EPG=90°，PF⊥EG，AB=BC=4，∠OEP=45°，

∴∠AEP+∠APE=90°，∠BPC+∠APE=90°，

∴∠AEP=∠BPC，

∴△APE∽△BCP，

∴，即，

解得：AE=；

（2）点O在AC上，理由：过点O分别作AD、AB的垂线，垂足分别为M、N,证得OM=ON，证得点O在∠BAD的平分线上，证得AC是∠BAD的平分线，所以，点O在AC上。

（3）设AP=x，则BP=4﹣x，由（1）可知：△APE∽△BCP，

∴，即 ，

解得：AE=x﹣x2=﹣（x﹣2）2+1，

∵AE+DE=AD=4，

∴DE=（x﹣2）2+3，

∴DE的最小值为3.