题目内容
(2012•本溪)如图,下图是一组由菱形和矩形组成的有规律的图案,第1个图中菱形的面积为S(S为常数),第2个图中阴影部分是由连接菱形各边中点得到的矩形和再连接矩形各边中点得到的菱形产生的,依此类推…,则第n个图中阴影部分的面积可以用含n的代数式表示为
.(n≥2,且n是正整数)

| S |
| 4n-1 |
| S |
| 4n-1 |

分析:观察图形发现第2个图形中的阴影部分的面积为
,第3个阴影部分的面积为
,依此类推,得到第n个图形的阴影部分的面积即可.
| s |
| 4 |
| s |
| 16 |
解答:解:观察图形发现:
第2个图形中的阴影部分的面积为
,
第3个图形中的阴影部分的面积为
,
…
第n个图形中的阴影部分的面积为
.
故答案为:
.
第2个图形中的阴影部分的面积为
| s |
| 4 |
第3个图形中的阴影部分的面积为
| s |
| 16 |
…
第n个图形中的阴影部分的面积为
| S |
| 4n-1 |
故答案为:
| S |
| 4n-1 |
点评:本题考查了图形的变化类问题,解题的关键是仔细的观察图形,找到规律用通项公式表示出来.

练习册系列答案
相关题目
 (2012•本溪)如图所示的几何体的俯视图是( )
(2012•本溪)如图所示的几何体的俯视图是( ) (2012•本溪)如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
(2012•本溪)如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?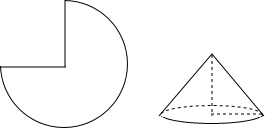 (2012•本溪)如图,用半径为4cm,弧长为6πcm的扇形围成一个圆锥的侧面,则所得圆锥的高为
(2012•本溪)如图,用半径为4cm,弧长为6πcm的扇形围成一个圆锥的侧面,则所得圆锥的高为 (2012•本溪)如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为
(2012•本溪)如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为