Question

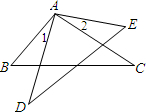如图，若AB=AE，∠1=∠2，则添加条件

AC

=

AD

，由“边角边”可得△ABC≌△AED．

Answer 1

分析：可添加条件：AC=AD，根据∠1=∠2，可得∠1+∠DAC=∠2+∠DAC，进而得到∠BAC=∠EAD，然后再加上条件AB=AE，AC=AD可利用SAS证明△ABC≌△AED．

解答：解：可添加条件：AC=AD，
∵∠1=∠2，
∴∠1+∠DAC=∠2+∠DAC，
即∠BAC=∠EAD，
在△ABC和△AED中

BA=AE ∠BAC=∠EAD AC=AD

，
∴△ABC≌△AED（SAS）．

点评：此题主要考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．