题目内容
 如图所示,正方形ABCD对角线交于O,点O是正方形A′B′C′O的一个顶点,两个正方形的边长都是2,那么正方形A′B′C′O绕O无论怎样转动时,图中两个正方形重叠部分的面积为________.
如图所示,正方形ABCD对角线交于O,点O是正方形A′B′C′O的一个顶点,两个正方形的边长都是2,那么正方形A′B′C′O绕O无论怎样转动时,图中两个正方形重叠部分的面积为________.
1
分析:求两个正方形重叠部分的面积,首先应证明:△AOE≌△BOF,从而将求重叠部分的面积转化为△AOB的面积.
解答:∵ABCD和A′B′C′O都是边长为2的正方形
∴OA=OB,∠AOB=∠A′OC′=90°,∠BAO=∠OBC=45°
∴∠AOB-∠BOE=∠A′OC′-∠BOE,即∠AOE=∠BOF
∴△AOE≌△BOF
∴重叠部分面积为:S△BOE+S△BOF=S△BOE+S△AOE=S△AOB= S正方形ABCD=
S正方形ABCD= ×22=1,
×22=1,
故答案为:1.
点评:通过将重叠部分的面积进行转化,再利用正方形的一些特殊性质,可使求解变的简单.
分析:求两个正方形重叠部分的面积,首先应证明:△AOE≌△BOF,从而将求重叠部分的面积转化为△AOB的面积.
解答:∵ABCD和A′B′C′O都是边长为2的正方形
∴OA=OB,∠AOB=∠A′OC′=90°,∠BAO=∠OBC=45°
∴∠AOB-∠BOE=∠A′OC′-∠BOE,即∠AOE=∠BOF
∴△AOE≌△BOF
∴重叠部分面积为:S△BOE+S△BOF=S△BOE+S△AOE=S△AOB=
 S正方形ABCD=
S正方形ABCD= ×22=1,
×22=1,故答案为:1.
点评:通过将重叠部分的面积进行转化,再利用正方形的一些特殊性质,可使求解变的简单.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
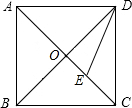 如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )
如图所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为( )A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|
 4、如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
4、如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )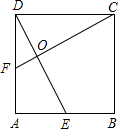 如图所示,正方形ABCD中,E为AB中点,F为AD中点,DE、CF交于O点,求证:DE⊥CF.
如图所示,正方形ABCD中,E为AB中点,F为AD中点,DE、CF交于O点,求证:DE⊥CF. 如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是
如图所示,正方形ABCD的边长为1,点E为AB的中点,以E为圆心,1为半径作圆,分别交AD,BC于M,N两点,与DC切于点P,则图中阴影部分面积是 如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
如图所示的正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: