题目内容
【题目】如图,已知![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() 、
、![]() 为直线
为直线![]() 上两点,且满足
上两点,且满足![]() ,连接
,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
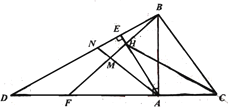
(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)若点![]() 是线段
是线段![]() 上的动点,连
上的动点,连![]() 并延长交
并延长交![]() 于
于![]() ,当
,当![]() 在线段
在线段![]() 的什么位置上时,
的什么位置上时,![]() ?请说明理由;
?请说明理由;
(3)在(2)的结论下,判断线段![]() 、
、![]() 、
、![]() 的数量关系.请说明理由.
的数量关系.请说明理由.
【答案】(1)3;(2)M在线段BF的中点时,![]() .理由见详解;(3)
.理由见详解;(3)![]() ,理由见详解
,理由见详解
【解析】
(1)根据已知条件可得出![]() ,有
,有![]() ,即可求出DE的值;
,即可求出DE的值;
(2)M在线段BF的中点,根据等腰直角三角形的三线合一以及已知以及证明![]() 即可;
即可;
(3)![]() ,由第2问可知
,由第2问可知![]() ,再求出
,再求出![]() 即可,证明
即可,证明![]() 可得出
可得出![]() .
.
解:(1)∵![]() ,
, ![]() ,
,![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]() ;
;
(2)当点M在线段BF的中点时,![]() .理由如下:
.理由如下:
∵![]() 为等腰直角三角形,点M在线段BF的中点
为等腰直角三角形,点M在线段BF的中点
∴![]() ,
,![]() ,
, ![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
(3)![]() ,理由如下:
,理由如下:
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
即![]() .
.

练习册系列答案
相关题目