题目内容
 如图所示的直角坐标系中,四边形ABCD各顶点的坐标分别为A(0,0)、B(9,0)、C(7,5)、D(2,7).求四边形ABCD的面积.
如图所示的直角坐标系中,四边形ABCD各顶点的坐标分别为A(0,0)、B(9,0)、C(7,5)、D(2,7).求四边形ABCD的面积.
分析:本题应利用分割法,把四边形分割成两个三角形加上一个梯形后再求面积.
解答: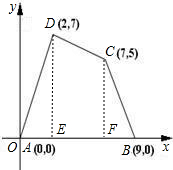 解:过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:
解:过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:
S=S△OED+SEFCD+S△CFB
=
×AE×DE+
×(CF+DE)×EF+
×FC×FB.
=
×2×7+
×(7+5)×5+
×2×5=42.
故四边形ABCD的面积为42平方单位.
 解:过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:
解:过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:S=S△OED+SEFCD+S△CFB
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故四边形ABCD的面积为42平方单位.
点评:主要考查了点的坐标的意义以及与图形相结合的具体运用.要掌握两点间的距离公式和图形有机结合起来的解题方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
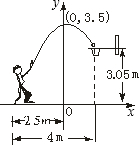 如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.建立如图所示的直角坐标系,则抛物线的表达式为
如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.建立如图所示的直角坐标系,则抛物线的表达式为 58、丁丁推铅球的出手高度为1.6m,在如图所示的直角坐标系中,铅球运动轨迹是抛物线y=-0.1(x-k)2+2.5,求铅球的落点与丁丁的距离.
58、丁丁推铅球的出手高度为1.6m,在如图所示的直角坐标系中,铅球运动轨迹是抛物线y=-0.1(x-k)2+2.5,求铅球的落点与丁丁的距离.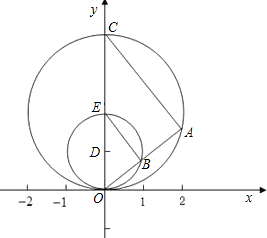 角形?若存在,求出点P的坐标;若不存在,说明其理由.
角形?若存在,求出点P的坐标;若不存在,说明其理由. 已知:如图,等腰△ABC的腰长为2
已知:如图,等腰△ABC的腰长为2 18、在边长为1的方格纸上建立如图所示的直角坐标系,把△ABC向下平移6个单位长度,得到△A1B1C1,画从出△A1B1C1,并作出△A1B1C1关于y轴对称的△A2B2C2,并直接写出点A2,B2,C2的坐标.
18、在边长为1的方格纸上建立如图所示的直角坐标系,把△ABC向下平移6个单位长度,得到△A1B1C1,画从出△A1B1C1,并作出△A1B1C1关于y轴对称的△A2B2C2,并直接写出点A2,B2,C2的坐标.