题目内容
观察等式找规律:
①a1=22-1=1×3;
②a2=42-1=3×5;
③a3=62-1=5×7;
…
(1)写出表示a4,a5的等式;
(2)写出表示an的等式(用字母n表示);
(3)求
+
+
+…
的值.
①a1=22-1=1×3;
②a2=42-1=3×5;
③a3=62-1=5×7;
…
(1)写出表示a4,a5的等式;
(2)写出表示an的等式(用字母n表示);
(3)求
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
分析:(1)根据a1,a2,a3的值,可直接得出a4和a5的值;
(2)根据a1=(2×1)2-1=(2-1)×(2+1),a2=(2×2)2-1=(4-1)×(4+1),找出规律,可得出an=(2×n)2-1=4n2-1=(2n-1)(2n+1);
(3)根据(2)得出的规律,再找出
,
,
的式子规律,分子不变,为1,分母是两个连续奇数的乘积,它们与式子序号之间的关系为:序号的2倍减1和序号的2倍加1,根据这规律把数代入计算即可.
(2)根据a1=(2×1)2-1=(2-1)×(2+1),a2=(2×2)2-1=(4-1)×(4+1),找出规律,可得出an=(2×n)2-1=4n2-1=(2n-1)(2n+1);
(3)根据(2)得出的规律,再找出
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
解答:解:(1)∵a1=22-1=1×3;a2=42-1=3×5;a3=62-1=5×7;
∴a4=82-1=7×9;
a5=102-1=9×11;
(2)∵a1=(2×1)2-1=(2-1)×(2+1),
a2=(2×2)2-1=(4-1)×(4+1),
a3=(2×3)2-1=(6-1)×(6+1),
…,
an=(2×n)2-1=4n2-1=(2n-1)(2n+1);
(3)∵a1=22-1=1×3;a2=42-1=3×5;a3=62-1=5×7;
=
=
=
(1-
);
=
=
×(
-
);
=
=
×(
-
);
∴
+
+
+…
=
×(1-
)+
×(
-
)+…+
×(
-
),
=
×(1-
+
-
+…+
-
),
=
×(1-
),
=
.
∴a4=82-1=7×9;
a5=102-1=9×11;
(2)∵a1=(2×1)2-1=(2-1)×(2+1),
a2=(2×2)2-1=(4-1)×(4+1),
a3=(2×3)2-1=(6-1)×(6+1),
…,
an=(2×n)2-1=4n2-1=(2n-1)(2n+1);
(3)∵a1=22-1=1×3;a2=42-1=3×5;a3=62-1=5×7;
| 1 |
| a1 |
| 1 |
| 3 |
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| a2 |
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| a3 |
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a2013 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 4025 |
| 1 |
| 4027 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 4025 |
| 1 |
| 4027 |
=
| 1 |
| 2 |
| 1 |
| 4027 |
=
| 2013 |
| 4027 |
点评:此题考查了数字的变化类,是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目

 +
+ +
+ +…
+…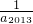 的值.
的值.