题目内容
如图，已知D是△ABC内一点，且DB=DC，∠ABD=∠ACD，求证：AB=AC．考点：等腰三角形的判定与性质
专题：证明题
分析：根据等边对等角得出∠DBC=∠DCB，进而得出∠ABC=∠ACB，然后根据等角对等边即可证得结论．
解答：证明：∵DB=DC，
∴∠DBC=∠DCB，
∵∠ABD=∠ACD，
∴∠ABD+∠DBC=∠ACD+∠DCB，
即∠ABC=∠ACB，
∴AB=AC．
∴∠DBC=∠DCB，
∵∠ABD=∠ACD，
∴∠ABD+∠DBC=∠ACD+∠DCB，
即∠ABC=∠ACB，
∴AB=AC．
点评：本题考查了等腰三角形的判定和性质，等边对等角、等角对等边是解题的关键．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
已知点A的坐标为（3，1），⊙A与坐标轴有三个公共点．在如图所示的平面直角坐标系中画出⊙A，并求⊙A的半径．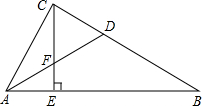
如图，在Rt△ABC中，∠ACB=90°，AD平分∠BAC，交BC于点D，CE⊥AB，垂足为E，交AD于点F，试猜想△CFD的形状，证明你的结论．