Question

已知A（-1，2）和B（-3，-1）．试在y轴上确定一点P，使其到A、B的距离和最小，求P点的坐标．

Answer 1

分析：作出B点关于y轴的对称点B′，连接AB′交y轴于点P，由两点之间线段最短可知，点P即为所求点，用待定系数法求出过AB′的一次函数解析式，再求出此函数与y轴的交点即可．

解答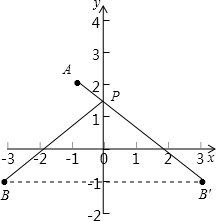：解：如图所示，出B点关于y轴的对称点B′，连接AB′交y轴于点P，
设过A、B′两点的一次函数解析式为y=kx+b（k≠0），
则

2=-k+b -1=3k+b

，解得k=-

3

4

，b=

5

4

，
故此一次函数的解析式为：y=-

3

4

x+

5

4

，当x=0时，y=

5

4

，故P点坐标
为（0，

5

4

）．
故答案为：P（0，

5

4

）．

点评：本题考查的是最短路线问题及一次函数的有关知识，有一定的综合性，但难易适中．