题目内容
不论b为何值,一次函数y=-2x+b2+4b+m的图象与y轴的交点总在正半轴上,则m的取值范围为 .
考点:一次函数图象上点的坐标特征
专题:
分析:将x=0代入y=-2x+b2+4b+m,得到图象与y轴的交点坐标为(0,b2+4b+m),要想交点总在正半轴上,只需b2+4b+m>0,即△=16-4m<0即可.
解答:解:将x=0代入y=-2x+b2+4b+m,
得y=b2+4b+m,
解图象与y轴的交点坐标为(0,b2+4b+m),
∵一次函数y=-2x+b2+4b+m的图象与y轴的交点总在正半轴上,
∴b2+4b+m>0,
∴△=16-4m<0,
解得m>4.
故答案为m>4.
得y=b2+4b+m,
解图象与y轴的交点坐标为(0,b2+4b+m),
∵一次函数y=-2x+b2+4b+m的图象与y轴的交点总在正半轴上,
∴b2+4b+m>0,
∴△=16-4m<0,
解得m>4.
故答案为m>4.
点评:本题考查了一次函数图象上点的坐标特征,在函数的图象上的点一定满足函数的解析式,同时考查了二次函数的性质.

练习册系列答案
相关题目
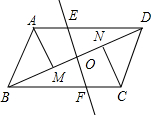 如图,?ABCD中,O是对角线BD中点,过点O的直线和AD、BC分别相交于E、F,AM平分∠BAD,CN平分∠DCB.请在平行四边形ABCD的基础上添加适当的条件,构造新的平行四边形,进而谈谈你的感想.
如图,?ABCD中,O是对角线BD中点,过点O的直线和AD、BC分别相交于E、F,AM平分∠BAD,CN平分∠DCB.请在平行四边形ABCD的基础上添加适当的条件,构造新的平行四边形,进而谈谈你的感想. 如图,矩形ABCD中,AB=6cm,AC=10cm,有一动点P,从点B开始,沿由B向A,再由A向D,再由D向C的方向运动,已知每秒钟点P的运动方向距离为2cm,试求△PBC的面积S(cm2)与运动时间t(秒)的函数关系式,并写出自变量t的取值范围.
如图,矩形ABCD中,AB=6cm,AC=10cm,有一动点P,从点B开始,沿由B向A,再由A向D,再由D向C的方向运动,已知每秒钟点P的运动方向距离为2cm,试求△PBC的面积S(cm2)与运动时间t(秒)的函数关系式,并写出自变量t的取值范围.