题目内容
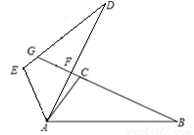
（10分）如图所示，△ABC≌△ADE，且∠CAD=10°，∠D=25°，∠EAB=120°，求∠DFB的度数．
【解析】
∵△ABC≌△ADE，∠D=25°
∴∠B=∠D=25°
∠EAD=∠CAB
∵∠EAB=∠EAD+∠CAD+∠CAB=120°
∠CAD=10°
∴∠CAB=
×（120°-10°）=55°
∴∠FAB=∠CAB+∠CAD=55°+10°=65°
又∵∠DFB是△ABF的外角
∴∠DFB=∠B+∠FAB
∴∠DFB=25°+65°=90°
【解析】
试题分析：由△ABC≌△ADE，可得∠EAD=∠CAB，根据已知条件可求得∠FAB的度数，再根据三角形外角性质可得∠DFB=∠FAB+∠B，即可求得∠DFB的度数.
考点：全等三角形的性质，三角形的外角性质.
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=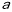
,其中
论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由．
直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．
C．
D．6 
无意义．