题目内容
矩形ABCD的对角线AC与BD相交于点O,AD=2AB=4,现有一直角三角板的直角顶点放在点O处,直角三角板的两边与矩形ABCD的边交于点E,F,如果OE=a,用a的代数式表示出所有可能的OF的值________.

2,2a,![]()
解析:解:①当F为CD的中点时,OE=FC=FD=a=1,
∵O为BD的中点,∴OF∥BC,
∴△DFO∽△DCB,则![]() =
=![]() ,OF=2,
,OF=2,
②当F不是CD的中点时,作OM⊥BC,ON⊥CD,垂足分别为M、N,
∵∠MON=∠EOF=90°,
∴∠MOE=∠NOF,
∴△OME∽△ONF,![]() =
=![]() =2,OF=2a,
=2,OF=2a,
③当F与C点重合时,过O点作OG⊥OC,交BC于G点,
OF=OC=AC=![]() =
=![]() =
=![]() .
.
故答案为:2,2a,![]()

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

 如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为
如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为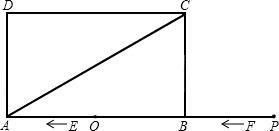 如图,矩形ABCD中,AB=6,BC=2
如图,矩形ABCD中,AB=6,BC=2 已知:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=5cm,则矩形对角线的长是
已知:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=5cm,则矩形对角线的长是