Question

【题目】如图①，在正方形ABCD中，AB＝6，M为对角线BD上任意一点（不与B、D重合），连接CM，过点M作MN⊥CM，交线段AB于点N

（1）求证：MN＝MC；

（2）若DM：DB＝2：5，求证：AN＝4BN；

（3）如图②，连接NC交BD于点G．若BG：MG＝3：5，求NGCG的值．

Answer 1

【答案】（1）见解析；（2）见解析；（3）CGNG＝．

【解析】

（1）作ME∥AB、MF∥BC，证四边形BEMF是正方形得ME=MF，再证∠CME=∠FMN，从而得△MFN≌△MEC，据此可得证；

（2）由FM∥AD，EM∥CD知＝＝＝，据此得AF=2.4，CE=2.4，由△MFN≌△MEC知FN=EC=2.4，AN=4.8，BN=6-4.8=1.2，从而得出答案；

（3）把△DMC绕点C逆时针旋转90°得到△BHC，连接GH，先证△MCG≌△HCG得MG=HG，由BG：MG=3：5可设BG=3a，则MG=GH=5a，继而知BH=4a，MD=4a，由DM+MG+BG=12a=6得a=，知BG=，MG=，证△MGC∽△NGB得，从而得出答案．

解：（1）如图①，过M分别作ME∥AB交BC于E，MF∥BC交AB于F，

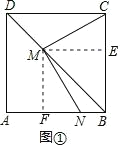
则四边形BEMF是平行四边形，

∵四边形ABCD是正方形，

∴∠ABC＝90°，∠ABD＝∠CBD＝∠BME＝45°，

∴ME＝BE，

∴平行四边形BEMF是正方形，

∴ME＝MF，

∵CM⊥MN，

∴∠CMN＝90°，

∵∠FME＝90°，

∴∠CME＝∠FMN，

∴△MFN≌△MEC（ASA），

∴MN＝MC；

（2）由（1）得FM∥AD，EM∥CD，

∴＝＝＝，

∴AF＝2.4，CE＝2.4，

∵△MFN≌△MEC，

∴FN＝EC＝2.4，

∴AN＝4.8，BN＝6﹣4.8＝1.2，

∴AN＝4BN；

（3）如图②，把△DMC绕点C逆时针旋转90°得到△BHC，连接GH，

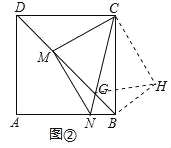
∵△DMC≌△BHC，∠BCD＝90°，

∴MC＝HC，DM＝BH，∠CDM＝∠CBH＝45°，∠DCM＝∠BCH，

∴∠MBH＝90°，∠MCH＝90°，

∵MC＝MN，MC⊥MN，

∴△MNC是等腰直角三角形，

∴∠MNC＝45°，

∴∠NCH＝45°，

∴△MCG≌△HCG（SAS），

∴MG＝HG，

∵BG：MG＝3：5，

设BG＝3a，则MG＝GH＝5a，

在Rt△BGH中，BH＝4a，则MD＝4a，

∵正方形ABCD的边长为6，

∴BD＝6，

∴DM+MG+BG＝12a＝6，

∴a＝，

∴BG＝，MG＝，

∵∠MGC＝∠NGB，∠MNG＝∠GBC＝45°，

∴△MGC∽△NGB，

∴＝，

∴CGNG＝BGMG＝．