��Ŀ����
Ϊ��ӭ�ӡ���•һ��С���ٵĹ���߷壮ij�˶�Ʒ��ר�����������ס��������˶�Ь�����мס��������˶�Ь�Ľ��ۺ��ۼ������
| �˶�Ь�۸� | �� | �� |
| ���ۣ�Ԫ/˫�� | m | m��20 |
| �ۼۣ�Ԫ/˫�� | 240 | 160 |
��֪����3600Ԫ���������˶�Ь����������3000Ԫ���������˶�Ь��������ͬ��
��1����m��ֵ��
��2��Ҫʹ�����ļס��������˶�Ь��200˫������������=�ۼ۩����ۣ�������21600Ԫ���Ҳ�����22440Ԫ���ʸ�ר�����ж����ֽ���������
�����㡿��ʽ���̵�Ӧ�ã�һԪһ�β���ʽ���Ӧ�ã�
����������1�����ܼ۳��Ե��۱�ʾ������Ь����������������Ь����������г�������⼴�ɣ�
��2���蹺�������˶�Ьx˫����ʾ�������˶�Ь˫��Ȼ������������г�һԪһ�β���ʽ���������ʽ��Ľ⼯���ٸ���Ь��˫������������ɣ�
�����.�⣺��1���������
 ��
��
�����ã�3600��m��2��=3000m��
���m=120��
�����飬m=120��ԭ��ʽ���̵Ľ⣬
���ԣ�m=120��
��2���蹺�������˶�Ьx˫���������˶�Ь˫��
��������ã�
 ��
��
����ʽ��Ľ⼯��160��x��174��
��x����������174��160+1=15��
���15�ַ�����
��

 ������������� ( )
������������� ( )
 D��3
D��3


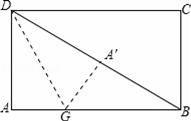

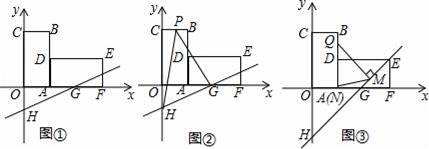

 �ϵĺ���
�ϵĺ��� ��ͼ������ͼ��ʾ����
��ͼ������ͼ��ʾ���� ��
�� 
