题目内容
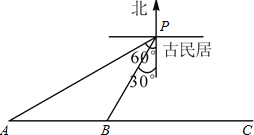
【题目】如图，在四边形ABCD中，AB=AC，BC=BD，若
，则
______.（用含
的代数式）.
【答案】
【解析】
延长DA到E点，使AE=AC，连接BE，易证∠EAB=∠BAC，可得△AEB≌△ABC，则∠E=∠ACB=
，BE=BC=BD，则∠BDE=∠E= ，可证∠DBC=∠DAC=4-180°，即可求得∠BCD的度数.
延长DA到E点，使AE=AC，连接BE
∵AB=AC， 
∴∠ACB =∠ABC = ，∠BAD=2
∴∠BAC =180°-2，∠EAB=180°-2
又AB=AB
∴△AEB≌△ABC（SAS）
∴∠E=∠ACB=，BE=BC=BD
∴∠BDE=∠E=
∴∠DBC=∠DAC=∠BAD-∠BAC=2-（180°-2）= 4-180°
∴∠BCD=
故答案为：
练习册系列答案
相关题目
【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题：
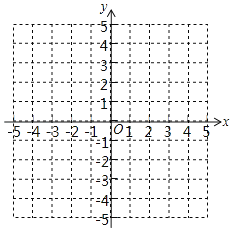
（1）在平面直角坐标系中，画出函数y＝|x|的图象：
①列表填空：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
|
|
| … |
②描点、连线，画出y＝|x|的图象；
（2）结合所画函数图象，写出y＝|x|两条不同类型的性质；
（3）结合所画函数图象，求方程|x|﹣2x﹣1＝0的解．
