题目内容
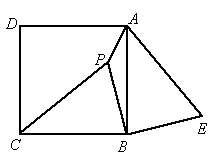
(2005·厦门)已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP,
(1)求证:△CPB≌AEB;
(2)求证PB⊥BE;
(3)若PA∶PB=1∶2,∠APB=135°,求cos∠PAE的值.
答案:略
解析:
解析:
|
解法 1 (1)证明∵四边形ABCD是正方形∴BC=AB ∵∠CBP=∠ABE BP=BE ∵△CBP≌△ABE (2)∵证明∠CBP=∠ABE ∴∠PBE=∠ABE+∠ABP=∠CBP+∠ABP=90° ∴PB⊥BE 解法 2(1)、(2)两小题可以一起证明. 证明:∵∠CBP=∠ABE ∴∠PBE=∠ABE+∠ABP=∠CBP+∠ABP=90° ∴PB⊥BE 以B为旋转中心,把△CBP按顺时针方向旋转90°, ∵BC=AB ∠CBA=∠PBE=90° BE=BP ∴△CBP与△ABE重合 ∴△CBP≌△ABE 解 (3)连接PE∵BE=BP ∠PBE=90° ∴∠BPE=45° 设 AP为k,则BP=BE=2k∴ 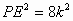 ∴ ∴
∵∠BPA=135° ∠BPE=45° ∴∠APE=90°∴AE=3k 在直角 △APE中: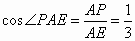 . . |

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
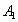 、
、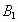 的坐标分别是________.
的坐标分别是________.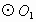 与
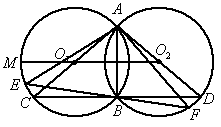
与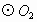 相交于点A、B,过点B作CD⊥AB,分别交
相交于点A、B,过点B作CD⊥AB,分别交 与
与 于点C、D.
于点C、D. 的直径.
的直径.
 ,求证:四边形是平行四边形;
,求证:四边形是平行四边形;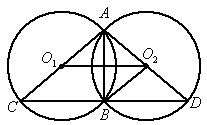
 在
在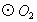 外,延长
外,延长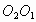 交
交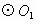 于点M,在劣弧
于点M,在劣弧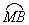 上任取一点E(点E与点B不重合).EB的延长线交优弧
上任取一点E(点E与点B不重合).EB的延长线交优弧 于点F,如图所示.连接AE、AF.则AE________AB(请在横线上填“≥、≤、<、>”这四个不等号中的一个=并加以证明.
于点F,如图所示.连接AE、AF.则AE________AB(请在横线上填“≥、≤、<、>”这四个不等号中的一个=并加以证明.