题目内容
若一次函数y=kx-4与两坐标所围成的三角形的面积是12,则此函数的表达式为 .
考点:一次函数图象上点的坐标特征
专题:
分析:由直线的性质可知,当x=0时,可知函数与y轴的交点为(0,-4),设图象与x轴的交点到原点的距离为a,根据三角形的面积为12,求出a的值,从而求出k的值,即可求得函数的表达式.
解答:解:当x=0时,可知函数与y轴的交点为(0,-4),
设图象与x轴的交点到原点的距离为a,
则
×4a=12,
a=6.
则函数与x轴的交点为(6,0)或(-6,0).
把(6,0)代入y=kx-4得,6k-4=0,k=
;
把(-6,0)代入y=kx-4得,-6k-4=0,k=-
.
所以此函数的表达式为y=
x-4或y=-
x-4,
故答案为y=
x-4或y=-
x-4.
设图象与x轴的交点到原点的距离为a,
则
| 1 |
| 2 |
a=6.
则函数与x轴的交点为(6,0)或(-6,0).
把(6,0)代入y=kx-4得,6k-4=0,k=
| 2 |
| 3 |
把(-6,0)代入y=kx-4得,-6k-4=0,k=-
| 2 |
| 3 |
所以此函数的表达式为y=
| 2 |
| 3 |
| 2 |
| 3 |
故答案为y=
| 2 |
| 3 |
| 2 |
| 3 |
点评:此题考查了一次函数图象上点的坐标特征,及直线与坐标轴的交点问题,解答时要注意进行分类讨论.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 如图所示,已知∠ADC+∠ABC=180°,DC=BC.求证:点C在∠DAB的角平分线上.
如图所示,已知∠ADC+∠ABC=180°,DC=BC.求证:点C在∠DAB的角平分线上.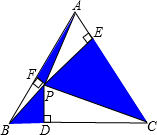 如图,P为边长为2的正三角形中任意一点,连接PA、PB、PC.过P点分别作三边的垂线,垂足分别为D、E、F,则PD+PE+PF=
如图,P为边长为2的正三角形中任意一点,连接PA、PB、PC.过P点分别作三边的垂线,垂足分别为D、E、F,则PD+PE+PF=