题目内容
 如图,?ABCD的顶点A,B的坐标分别是A(-3,0)、B(0,1),顶点C、D在双曲线y=
如图,?ABCD的顶点A,B的坐标分别是A(-3,0)、B(0,1),顶点C、D在双曲线y=| k |
| x |
-
| 63 |
| 16 |
-
.| 63 |
| 16 |
分析:过D作DF⊥x轴,过D作x轴的平行线,过C作y轴平行线,两线交于P点,可得出三角形AOB与三角形DCP全等,由全等三角形的对应边相等得到DP=AO,CP=BO,由A与B的坐标得出OA与OB的长,确定出DP与CP的长,由已知四边形BCDE的面积为三角形ABE面积的2.5倍,得出平行四边形ABCD的面积为三角形ABE面积的3.5倍,而三角形ABE与平行四边形的高为一条高,可得出AE与AD的比值,由三角形AOE与三角形AFD相似,根据相似得比例,得到AO与AF之比,由AO的长求出AF的长,由AF-OA求出OF的长,即为D的横坐标,代入反比例函数解析式中表示出D的纵坐标,进而由DP与CP表示出C的坐标,代入反比例解析式中得到关于k的方程,求出方程的解即可得到k的值.
解答: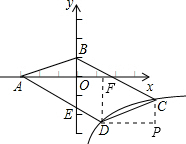 解:过D作DF⊥x轴,过D作x轴的平行线,过C作y轴平行线,两线交于P点,
解:过D作DF⊥x轴,过D作x轴的平行线,过C作y轴平行线,两线交于P点,
可得△AOB≌△DCP,由A(-3,0),B(0,1),得到DP=AO=3,CP=BO=1,
∵S四边形BCDE=2.5S△ABE,且S平行四边形ABCD=S四边形BCDE+S△ABE,
∴S平行四边形ABCD=3.5S△ABE,
又∵△ABE与平行四边形ABCD高为同一条高,
∴AE:AD=4:7,
∵∠AOE=∠AFD=90°,∠OAE=∠FOD,
∴△AOE∽△AFD,
∴AO:AF=AE:AD=4:7,又AO=3,
∴AF=
,即OF=
-3=
,
设D(
,
),则C(
,1+
),
将C坐标代入反比例解析式得:
×(1+
)=k,
解得:k=-
.
故答案为:-
.
 解:过D作DF⊥x轴,过D作x轴的平行线,过C作y轴平行线,两线交于P点,
解:过D作DF⊥x轴,过D作x轴的平行线,过C作y轴平行线,两线交于P点,可得△AOB≌△DCP,由A(-3,0),B(0,1),得到DP=AO=3,CP=BO=1,
∵S四边形BCDE=2.5S△ABE,且S平行四边形ABCD=S四边形BCDE+S△ABE,
∴S平行四边形ABCD=3.5S△ABE,
又∵△ABE与平行四边形ABCD高为同一条高,
∴AE:AD=4:7,
∵∠AOE=∠AFD=90°,∠OAE=∠FOD,
∴△AOE∽△AFD,
∴AO:AF=AE:AD=4:7,又AO=3,
∴AF=
| 21 |
| 4 |
| 21 |
| 4 |
| 9 |
| 4 |
设D(
| 9 |
| 4 |
| 4k |
| 9 |
| 21 |
| 4 |
| 4k |
| 9 |
将C坐标代入反比例解析式得:
| 21 |
| 4 |
| 4k |
| 9 |
解得:k=-
| 63 |
| 16 |
故答案为:-
| 63 |
| 16 |
点评:此考查了反比例函数综合题,涉及的知识有:相似三角形的判定与性质,全等三角形的判定与性质,坐标与图形性质,以及反比例函数的性质,熟练掌握性质是解本题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 下垂,如图②,求彩旗下垂时最低处离地面的最小高度h.
下垂,如图②,求彩旗下垂时最低处离地面的最小高度h. 如图,一铁路路基的横断面是等腰梯形ABCD,斜坡BC的坡度tanC=
如图,一铁路路基的横断面是等腰梯形ABCD,斜坡BC的坡度tanC= 如图,一铁路路基横断面为等腰梯形ABCD,斜坡BC的坡度i=1.5:1,路基高AE为2.5m,底CD宽为10m,求路基顶AB的宽.
如图,一铁路路基横断面为等腰梯形ABCD,斜坡BC的坡度i=1.5:1,路基高AE为2.5m,底CD宽为10m,求路基顶AB的宽. 18、如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?
18、如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?