题目内容
 在如图的方格纸上有A、B、C三点(每个小方格的边长为1个单位长度).
在如图的方格纸上有A、B、C三点(每个小方格的边长为1个单位长度).(1)在给出的直角坐标系中(或舍去该直角坐标系,在自己另建立适当的直角坐标系中),分别写出点A、B、C的坐标;
(2)根据你得出的A、B、C三点的坐标,求图象经过这三点的二次函数的解析式.
分析:本题主要考查二次函数解析式的确定、先在题目给出的坐标系中读出A、B、C三点的坐标,然后可用待定系数法求出抛物线的解析式.
解答:解:(1)点A的坐标为(2,3),点B的坐标为(4,1),点C的坐标为(8,9).
(2)设所求的二次函数解析式为:y=ax2+bx+c.
把点A、B、C的坐标代入抛物线的解析式中,
可得:
,
解得
,
∴所求的二次函数解析式为y=
x2-4x+9.
(答案不唯一,也可以A或B或C为原点创建新的坐标系进行求解)
(2)设所求的二次函数解析式为:y=ax2+bx+c.
把点A、B、C的坐标代入抛物线的解析式中,
可得:
|
解得
|
∴所求的二次函数解析式为y=
| 1 |
| 2 |
(答案不唯一,也可以A或B或C为原点创建新的坐标系进行求解)
点评:本题主要考查用待定系数法求二次函数解析式的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在如图的方格纸上有一个Rt△ABC,试着计算一下:是否一定有某两边的平方和等于第三边的平方?
在如图的方格纸上有一个Rt△ABC,试着计算一下:是否一定有某两边的平方和等于第三边的平方?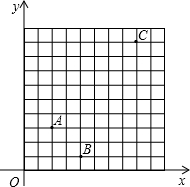 在如图的方格纸上有A、B、C三点(每个小方格的边长为1个单位长度).
在如图的方格纸上有A、B、C三点(每个小方格的边长为1个单位长度).
