题目内容
14.三角形两边的长分别是8和6,第三边的长是方程x2-12x+20=0的一个实数根,则三角形的周长是( )| A. | 24 | B. | 26或16 | C. | 26 | D. | 16 |
分析 易得方程的两根,那么根据三角形的三边关系,得到符合题意的边,进而求得三角形周长即可.
解答 解:∵x2-12x+20=0,即(x-2)(x-10)=0,
∴x-2=0或x-10=0,
解得:x=2或x=10,
当x=2时,三角形的三边2+6=8,不能构成三角新,舍去;
当x=10时,符合三角形三边之间的关系,其周长为爱6+8+10=24,
故选:A.
点评 此题考查了解一元二次方程-因式分解法和三角形三边关系,求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否成三角形的好习惯

练习册系列答案
相关题目
4.长为9,6,5,3的四根木条,选其中三根组成三角形,选法有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
2.平面直角坐标系中,点M(-3,2)到y轴的距离是( )
| A. | 3 | B. | 2 | C. | 3或2 | D. | -3 |
9.若关于x的方程$\frac{1}{x-1}$+$\frac{mx}{{x}^{2}-1}$=$\frac{2}{x+1}$有增根,则m的值为( )
| A. | 4 | B. | -2 | C. | 4或-2 | D. | 无法确定 |
19.下列图形中具有稳定性的是( )
| A. | 平行四边形 | B. | 等腰三角形 | C. | 长方形 | D. | 梯形 |
6.若x>y,则下列式子中错误的是( )
| A. | x-3>y-3 | B. | x+3>y+2 | C. | -3x>-3y | D. | $\frac{x}{3}>\frac{y}{3}$ |
12.若$\frac{a}{b}$=$\frac{2}{3}$,则$\frac{a}{a+b}$等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |




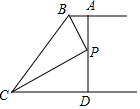 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是( )
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是( )